前言
攻略推荐和思路
这些攻略我觉得对想玩高难度的新手来说很有用:
施法者玩法入门讲解
主角build推荐
队友build推荐
不公平难度前期流程
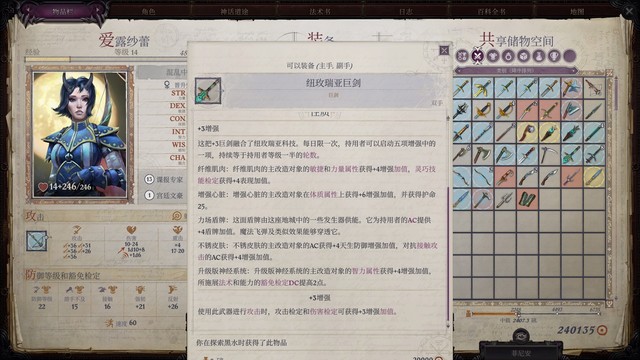
商人和值得购买的商品
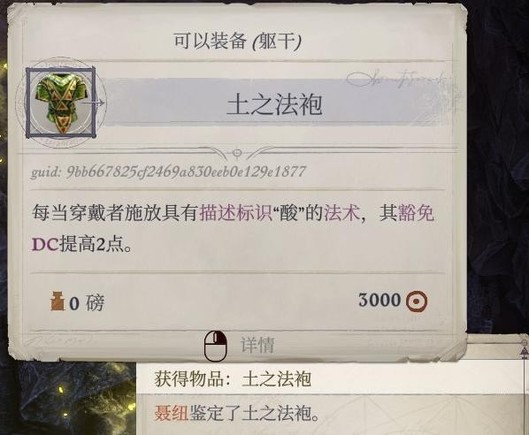
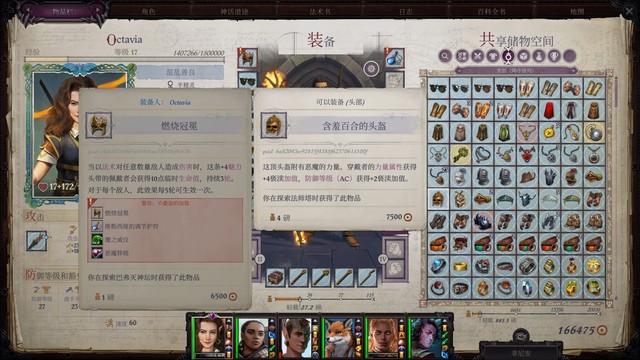
圣教军模式下圣器装备效果预览
在这些基础上,根据游戏更新改动和我自己的游戏习惯(偏好回合制)做了调整。
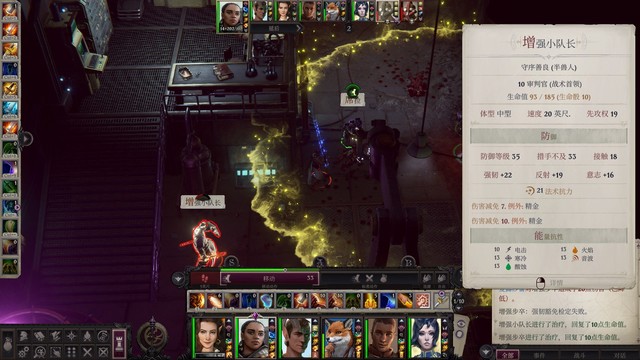
高难度下最好提前选好道途,选择和道途更相配的职业可以降低游戏难度,比如经典搭配:天使圣使、巫妖法爷、诡计大师剑圣。
不公平难度下,我会利用游戏系统来尽快提升战斗力并规避不想要的事件(毛经验和sl)、购入并抠门地使用一些低难度用不着的物资、根据队友战斗力与队伍搭配来选择队友、放弃rp选择更有利于战斗的对话选项……难度更低没必要照抄。亲测核心及以下难度不需要这些额外操作也能通关。
本流程会尽量做到全收集,最多只会跳过一些不是打不过而是打起来实在难受、没有好奖励也没有剧情的小怪。
开卡和毛经验
开卡
职业:术士-探寻者
种族:半精灵
有魅力加值
加点:14 12 14 10 22
技能:隐匿,沟通,世界
当时预计成型后的攻坚队伍配置是席拉+兰恩+柯米丽雅+索希尔+聂纽,因此技能要补上队友大概没有的隐匿,剩下两点是为了在岱兰第五章任务里骗它者和扎营做饭。
专长:
法术专攻-塑能
法术专攻效果:对应学派法术豁免难度+1。点塑能主要是为了打输出。
法术专攻-咒法
咒法主要用来打控制,聂纽已经专攻幻术了,聂纽控不住的就让主角控。
前期好用的咒法:油腻术、闪光尘、臭云术、次元陷坑……后期有aoe津波,如果有机会或许可以爽一爽。
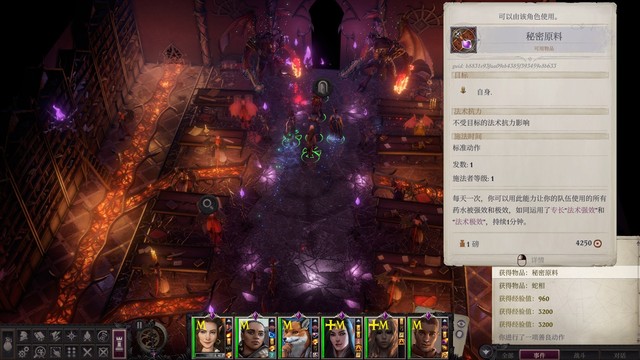
额外能力:奥法血承-奥法契约
作用是回复指定法术的使用次数,可以提升术士施法的灵活性+后期搭配灵使的刷新球。
出身:扒手
图的是先攻+2
法术:油腻术,渐隐术
奥法血承3级会送魔法飞弹,就不选了。缩小/变巨/法师护甲其他队友也能上,护盾术目前没必要。
初始阵营:混乱邪恶
只是为了能在第二章戴上限制非善良阵营的装备【德莱文的帽子】(赠送每天一次法术瞬发;智力+2亵渎加值。如果主角不是法师,可以给聂纽戴)
最终角色卡: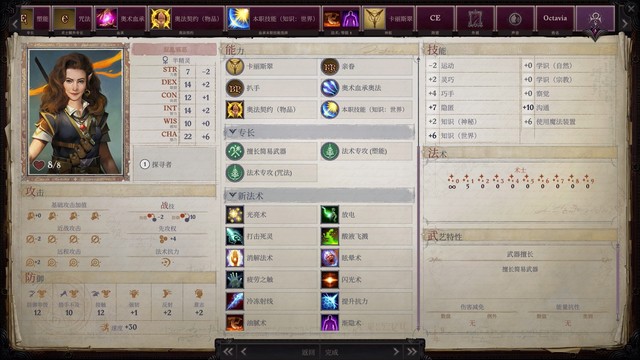
“毛经验”的方法
进游戏之前就在难度菜单勾选上仅活跃伙伴获得经验,在新队友马上要入队(对话框可以选结束对话)时,打开设置,关闭仅活跃队友获得经验选项,使新队友和主角的经验同步,对话结束新队友入队后再马上重新打开此选项。直到队伍满六人,之后就一直关闭此选项。
序章
第一场战斗前
如果想做飞升结局,要在应对德斯卡瑞时选择战斗(而不是防御)
见到席拉和安妮维亚,记得毛经验操作,对话和场景中的技能检定也一定要通过sl保证成功,不公平难度下每一丝经验都很重要!如果检定成功+毛经验操作成功,席拉入队后主角和席拉的经验应该都是1038/2000
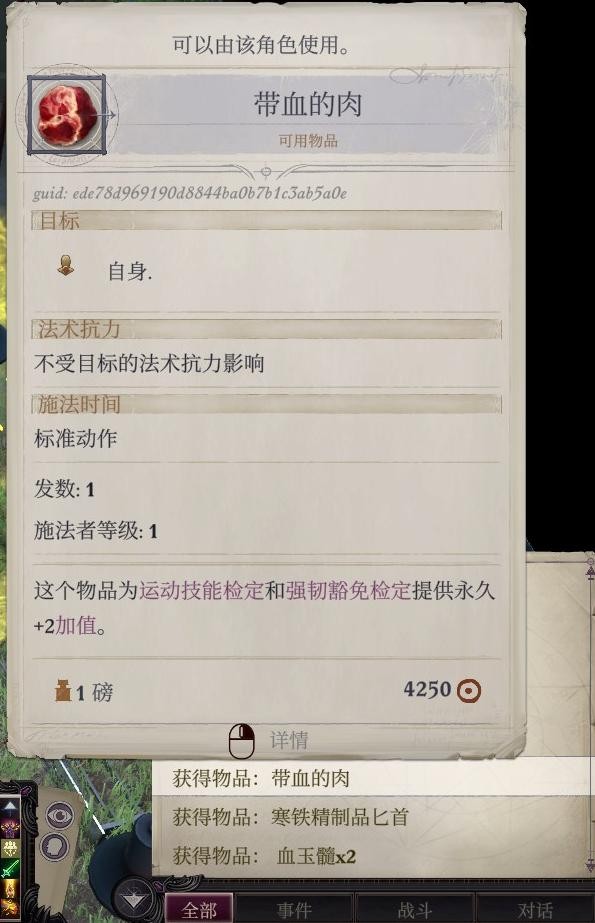
再往前捡到了一些装备和特伦迪利弗的鳞片。披风给席拉穿上,主角如果有需要可以拿一把武器,其他的都可以日后卖钱。从现在起要保证包里至少有一个鳞片,直到第一章把鳞片给说书人看。
柯米丽雅入队后三人的经验应该都是1413/2000。然后存档,接下来要战斗了
战斗
高难度下我比较喜欢玩回合制,不嫌麻烦的话最好关闭【自动结束回合】,因为这样才可以在整轮攻击后进行五尺快步、在施法者放法术之后再瞬发法术。
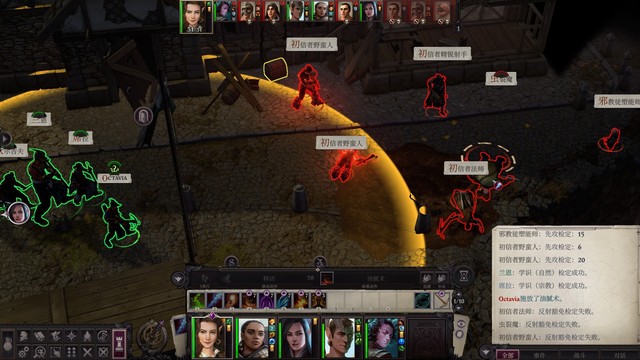
不公平难度下队友初始的命中率不高。遇到兰恩和雯朵格之前,战斗的思路是:延后其他队友的行动次序,使ac最高(也就是最不容易被普通物理攻击命中)的席拉第一个行动(记得开启席拉的防御式攻击),拉住敌人;通过调整队形和走位,尽量使安妮维亚在第一轮就加入战斗,让四级的安妮维亚射死敌人。
遇到兰恩和雯朵格
先选2. 我为什么要告诉你?,这样后续对话会有察觉检定,额外获得每人92经验,结束对话后可以升级了。升级后再与场景内物品互动,通过检定的概率会高一些。
接下来是拔剑剧情,选怒斥叛徒+惩治恶人,获得英雄气概buff,方便后续沟通检定。
对话后兰恩和雯朵格入队,目前经验是2349/5000。
我选择先选雯朵格打序章(给雯朵格的加点就只考虑序章强度),再在序章末尾选兰恩(给兰恩的加点就不考虑序章过渡了,直接升级转近战,这样更适合远程职业的主角)
2级加点
主角:职业不变,技能点的还是隐匿、世界、沟通
席拉:受诅巫师,察觉、灵巧、使用魔法装置、宗教,如果主角没点沟通也可以给席拉点沟通。野兔魔宠,冻皮,跛足或知命,缩小术+法师护甲(这样就可以自己上buff了)。记得在能力栏手动激活野兔魔宠
山茶:职业不变,巧手、灵巧,避灾
兰恩:不公平难度下禅宗射手的命中不太够,转近战拿斩矛。战士-突变斗士,运动、自然、察觉,猛力攻击
雯朵格:游荡者-大盗(为了要害打击),运动、灵巧、察觉
继续战斗
现在队伍就能打一些输出了,主要靠雯朵格的要害打击: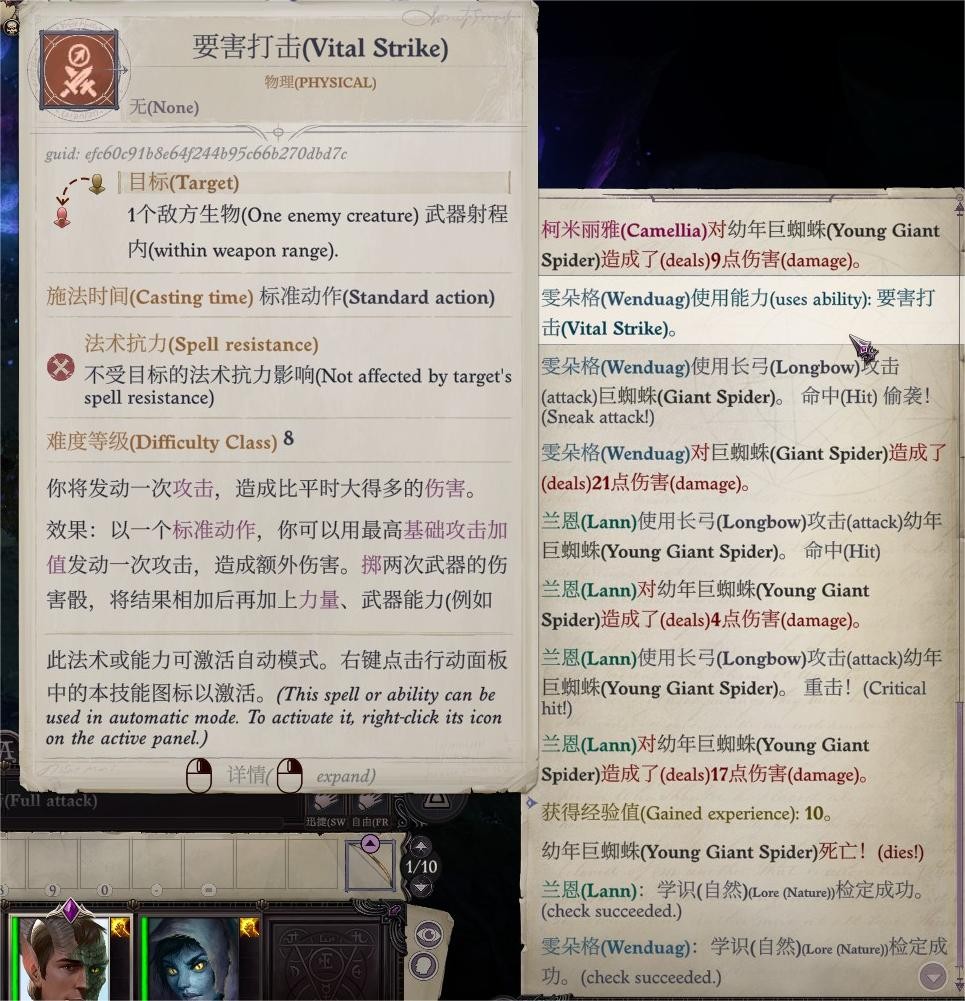
碎石堆后的小型土元素攻击加值比较高,同样可以调整走位让安妮维亚进战斗。也可以让柯米丽雅给雯朵格上变巨buff,主角先丢油腻术控住土元素,再给雯朵格渐隐术。打赢获得一个治疗轻伤魔杖。
到达混种人营地
到混种人营地后进入疲劳状态。对话不展示天堂之光,多获得300经验(导致雯朵格入队、兰恩离队)。
与霍尔格斯对话,sl通过交涉检定,预订第一章的启动资金。
搜刮完整个营地,和商人黛拉对话,卖出所有垃圾(可如图勾选),如果队内没有不死生物,造成轻伤卷轴也可以卖。购入卷轴英雄气概、朦胧术,此外我还买了祝福术+额外一张朦胧术+油腻术睡眠术各一张+法师护甲药水+防护邪恶/混乱药水+寒铁弹药箭筒

接下来根据剧情要休息,休息之前先调整法术,给山茶记变巨术+防护阵营×2+祝福术
休息后兰恩离队,走雯朵格指的路到盾牌迷宫门口,不急着进去,先把地图右侧的王蜥杀了拿经验。
盾牌迷宫1
目前的buff
全员:祝福术
席拉:防护邪恶、缩小术
雯朵格:变巨术
遇到第一波敌人,依旧保证席拉走在最前面+在我方第一个开始行动,t住,柯米丽雅给席拉上避灾,雯朵格用要害打击一个个杀,先杀法师。
法术用完了就休息,盾牌迷宫内不限制休息次数,还可以通过sl防止休息时被敌人偷袭。
卷轴和药水先不要用,之后打boss和精英怪再用。
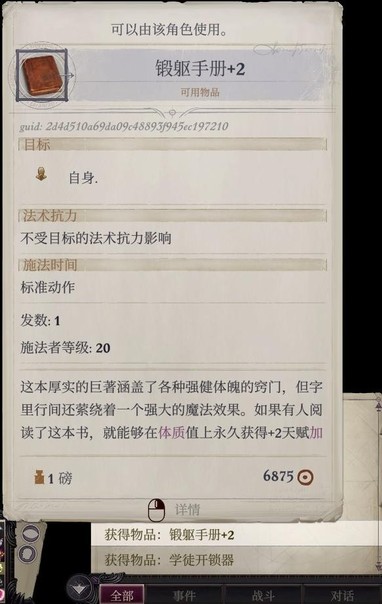
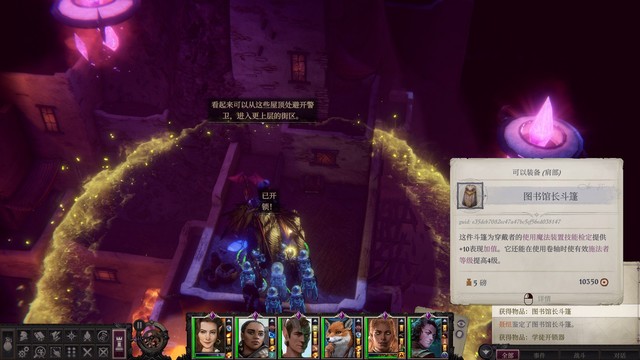
主角在背包栏阅读这本书,可以获得特殊加值。今后遇到相同分类下的书也都可以读,基本都能学到加值
清到这个程度就差不多升3级了(腐化混种人暴徒和水元素不好打,先不打,留着后面再来):
如果超重,可以把装备扔地上,最后再一并捡起来卖给商人
3级加点
主角:技能加点不变,法术专精-魔法飞弹;刺耳尖啸
席拉:武僧-传统武僧(比普通武僧+2意志豁免),灵巧、宗教、察觉、使用魔法装置,精通先攻、鹤形拳
山茶:技能加点不变,武器专攻-细剑
雯朵格:杀手,熟练偷袭者
升三级之后可以休息一下再继续,休息之前记得记法术,柯米丽雅二环记树肤(给席拉)、鹰之威仪(给席拉)、牛之蛮力(给雯朵格)(更新后新增了骨拳术,也是不错的群体buff,亲测核心及以下难度可以把树肤改成骨拳术,更高难度我没有试过,有兴趣可以试一下)
盾牌迷宫2
凶猛王蜥:可以让主角给雯朵格渐隐术、雯朵格用要害打击打措手不及,一箭一个
颜色解谜:黄蓝红黄,获得辉光
腐化混种人暴徒:上满全套buff之后席拉t住,有隐匿/渐隐术的雯朵格射他。其他小兵在3级队伍满buff状态下不难打
水元素
席拉buff:缩小术,虔诚护盾(药水)(席拉自带一个,序章可以捡到两个,省着用),树肤,抵抗寒冷药水,朦胧术也可以上一下(武器已经可以替换到寒铁精制品长剑了)
雯朵格buff:变巨术,雯朵格身上自带一瓶猫之轻灵药水,也可以喝了(武器已经可以替换到复合长弓)
全员buff:祝福术
首先席拉接近水元素,山茶不用动,主角和雯朵格走到能打到的位置就够了。第二轮开始席拉t住,山茶不断给席拉上避灾,雯朵格要害打击,主角不断给雯朵格上渐隐术(这样雯朵格的攻击检定要过的是水元素的措手不及ac而不是普通状态下的ac,更容易命中),渐隐术用完之后改对水元素用天使之光。每轮射十来点伤害就过了
盾牌迷宫boss和后续
打boss之前可以先把雯朵格身上不需要的东西扒下来,一会儿她就离队了。可以再休息一次然后再上一遍之前说的buff,打不过的话也可以把买的卷轴用了。
到boss房之后,选天使选项可以在第一章的伊斯绰德塔获得天使之貌(+元素抗性),这里为了抗性选天使选项
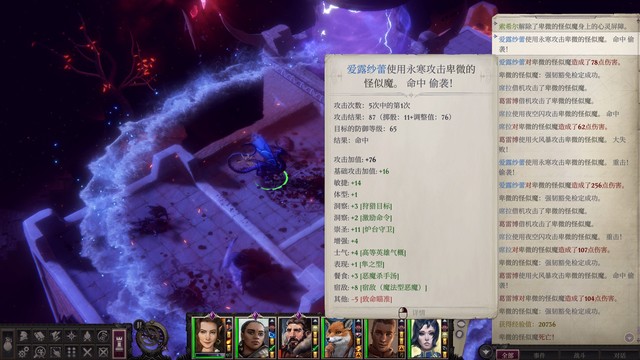
开局席拉第一个行动,辟邪斩+冲锋。然后主角往霍西拉脚下放油腻术,豁免难度18,对面反射豁免8。控不住其实也无所谓,对面打席拉是很难命中的(如图2),第一轮席拉ac有冲锋减值-2所以对方roll到18才能打中,之后更难打中。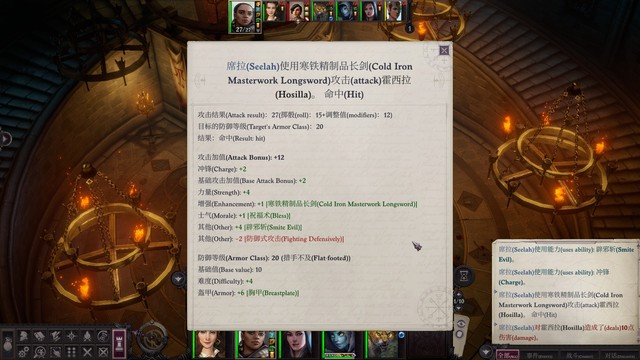
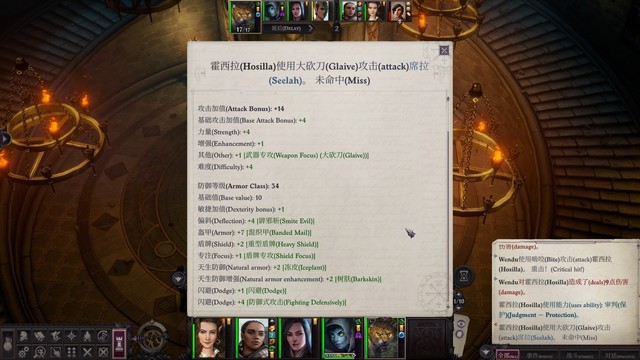
第二轮开始就又是主角给变巨雯朵格上渐隐术,射她。上了辟邪斩的席拉命中率高一些,可能也能打一些伤害。我运气比较好,第二轮雯朵格射完箭就打出后续剧情了。
然后出现两只怪似魔,席拉t住靠脆皮主角更近的那个,另一个离兰恩近,兰恩会t一下,随便打打就过了,兰恩倒了没事,会复活的。
打完让兰恩入队。把垃圾都卖给黛拉,捡到的决斗剑和标枪,如果主角不用的话,也可以卖掉。目前经验6747/9000,金币5203(卖了盗墓者盔甲和+1防御护腕),可能会比正常状态高点,因为休息时遇到了营地遇袭
兰恩升级加点:突变斗士,运动、自然、察觉,顺势斩、强力顺势斩。换上霍西拉掉的恐惧进击。
上楼之前又休息了一次
离开盾牌迷宫进入灰兵营
上地表直到遇到伊拉贝思之前都不需要上buff,之后也可以先不上,走在队伍后面,不加入战斗,让伊拉贝思和其他士兵在前面打,同样可以拿到经验。
上楼之前把地上的东西都捡了,这也是启动资金。
然后上buff,上楼直接开战,npc负责左侧,我们打右侧,远程优先打塑能师(因为ta优先攻击主角),席拉和主角对避灾需求不大的话,山茶也可以上去砍两下杂兵。 右侧有会放臭云术的赘行魔,嫌被控难受的话,可以在快进它视线范围内的时候停下来,等伊拉贝思那边的人打完左侧过来替我们吃。或者席拉先去骗它出招。这段战斗的重点不是输出而是少掉血。
右侧有会放臭云术的赘行魔,嫌被控难受的话,可以在快进它视线范围内的时候停下来,等伊拉贝思那边的人打完左侧过来替我们吃。或者席拉先去骗它出招。这段战斗的重点不是输出而是少掉血。
打完还是要把东西都捡了,超重也要捡
捡完上楼,buff应该还没消失,又是一群小怪+臭云术,我的打法:席拉抢到先攻先冲锋过去,兰恩第二个冲锋秒了一个赘行魔并使其他敌人进入恐惧状态,他们在这种小场地跑来跑去很容易吃到兰恩的借机攻击,这样就好打了。
打完还是捡了东西再上楼,冥娜蛊剧情杀,摆烂就行,抠门的话可以趁死前捡捡被冥娜蛊杀掉的小兵的装备
第一章
在铁卫雄心醒来
醒来后在酒馆和全部npc聊天并通过所有检定后应该能够:
发现伊斯绰德塔、提拉巴德的住处;
发现丝线工坊、黄玉必应屋;
酒馆老板处过宗教暗骰+5经验;
解锁皮塔克斯的酒窖;
伊拉贝思处过宗教暗骰+5经验;
因妲罗处选“容我解释一下”,检定成功+13经验和季斯卡之爪(+1炽焰短剑),卖掉+2075金币
发现黑翼图书馆;
发现寒溪村;
弗恩·秋雾处接任务;
霍尔格斯处获得2000金币,再次要求更高价,sl成功并接任务;
来到地下室,从左到右三个开关是上下下,然后再按最左边的按钮打开密室,拿到+2魅力头带给席拉

和沃尔吉夫对话接任务,把垃圾都捡了,上楼和伊拉贝思对话,把沃尔吉夫放出来
再到酒馆外面逛一圈把垃圾捡了卖了,顺便和乔兰对话给他看辉光
找牧师购入霜护戒指给席拉戴上,再买一张防护电击(丝线工坊用)、一张共用防护火焰(伊斯绰德塔用)、2级卷轴抄写工具(沃尔吉夫做卷轴用),辛辣油酥饼菜谱,还有需要的药水。买完之后包里有缩小术5、变巨术5
最终出门前的经验是9158/15000(正常情况经验应该再高一点,因为我有一段忘记毛经验了),金币58。
4级加点
在上面的过程中已经升4级了(没写的就是和以前一样)
主角:魅力,闪光尘
席拉:圣武士,魅力,宗教、察觉、使用魔法装置
山茶:敏捷,邪眼
兰恩:力量
沃尔吉夫:敏捷,灵巧、巧手、隐匿、神秘(可以做卷轴和聂纽互补法术)、察觉,学了克敌机先和猫之轻灵。用卷轴学护盾术(缩小术去黑翼图书馆捡卷轴学,在那之前先用药水) 沃尔吉夫任务
出门在大地图上可能会碰到随机刷出的遭遇战,遇到就打,为了经验和可能会掉的可以卖钱的垃圾。目前队伍4级,只有速袭魔比较难打,可以看到就读档。
到贼裔藏身处把对话过完,说会找到叛徒,离开,回铁卫雄心找伊拉贝思对话,离开,去古董奇宝店,获得菲尼安,进地下室和店主对话,回到贼裔藏身处,对话前存档,选梅荣,sl通过两次沟通检定,搜刮,回到铁卫雄心和沃尔吉夫对话完成任务(顺便卖垃圾)。目前经验9644,金币1679。
丝线工坊
到马尸,再到丝线工坊。先不去市集广场,去了就要接新队友,分经验的人就多了一个,所以先把其他地方打了
在丝线工坊的街道上,可以先给席拉上树肤和防护邪恶,席拉冲锋打野蛮人、沃尔吉夫冲锋打敌方远程(这样敌人抬手的时候可以被借机攻击),其他人照旧(山茶给席拉避灾、兰恩打席拉t住的怪、主角自由发挥)
进屋再给席拉用防护电击卷轴,席拉冲锋打门口野蛮人(主要是为了第一个进敌人视线拉仇恨),集火闪耀之拳,剩下的不难打。
打完把东西捡一下,拿到的头部装备主角不需要的话可以卖了。不屈护甲不确定后面有没有用,先留着。目前经验9966。
伊斯绰德塔
去之前可以先去同归于尽的决斗者。
进地图,不急着上buff,过剧情,和葛雷博对话,然后游戏会自动存档。全队潜行,从两边走,把柱子推倒,然后再上buff,能上的都可以上了(因为到下一个地图之后也该休息了),共用防护火焰卷轴也用掉,开战后技能也都可以用掉。
以前没提到过的可以上的新buff:兰恩的诱变剂(力量)、沃尔吉夫的法师护甲(因为目前都只能用一次所以没在丝线工坊用)
打完之后进塔内部,能捡的东西都捡了再走。和特尔顿对话,过宗教暗骰有6经验。
熟面孔成就:帮助并放走吃纸人。
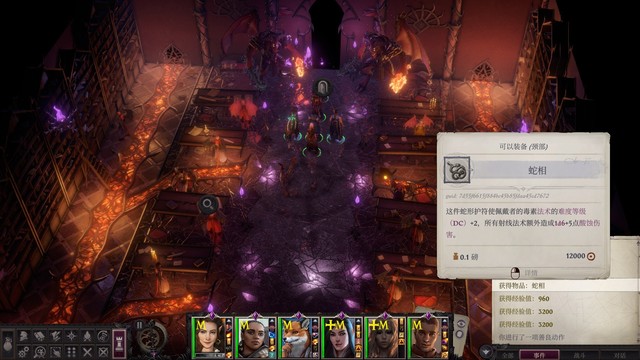
+1小圆盾和卡兰德拉女士的链甲衫可以给山茶换上,烈火xx硬头锤先留着不卖,安息之恩和诱捕长弓可以卖
目前经验10795
市集广场1
出地图,去市集广场,半路会进疲劳状态,到市集广场门口再休息。休息前记得改法术,而且这次休息要让沃尔吉夫做一张猫之轻灵卷轴,之前获得的管狐宠物可以提前给沃尔吉夫装备上,提升成功率
休息前改法术
柯米丽雅:变巨1防护阵营2祝福术2,树肤1牛之蛮力2凛冬之握1。这样持续时间每等级1分钟的buff都是双份(变巨术可以用魂契物+1),维持的时间长一点。凛冬之握是为了控多个敌人。
沃尔吉夫:法师护甲1护盾术2(还剩一个法术位,我选了七彩喷射,实际没用到),猫之轻灵2
进广场往前走两步遇到贼裔,选混乱选项敲诈获得112金币,然后再上buff:
目前满buff
席拉:树肤、防护邪恶(我懒得上缩小术了,不嫌麻烦最好上
兰恩:变巨、牛之蛮力、诱变剂(力量)
沃尔吉夫:法师护甲、护盾术、猫之轻灵
全员:祝福术
现在山茶除了给席拉上避灾之外,还可以给难打的敌人上邪眼降ac了
先把广场右下角那一块清掉(上下左右指的都是按M看到的地图里的位置),不接近小烬附近(否则小烬入队会多一个人分经验)、不去右下角和凯丽莎对话(为了抓紧时间利用buff),之后再来;地上的东西也都不用捡,等buff时间结束再一起捡起来,有用的留下,不用的可以再丢回地上(不然会超重,影响后续战斗),等下一次来市集广场再捡走。
打完之后到接近地图中心的位置完成运动检定,清出道路,往左走
市集广场2(+杀胡尔伦)
在遇到胡尔伦和拉米恩时我的buff持续时间也差不多结束了,对话中选择展现天堂之光。
对话后往上走,和紫色光互动拿到紫色石刀,开启御衡者道途。
再往上,看到敌人再上buff,这边广场敌人比较多,可以让山茶放凛冬之握。如果还是打不过也可以贴着左边走,绕过去,下次来再打。
广场旁边这个位置,不要再往p1的左上角走了,有集群,不好处理,等小烬入队再来:

上楼梯,杀死这里的憎美魔,在图中这个位置救魔裔: 追问是谁获得额外经验,然后过运动检定救人,sl通过检定,让他们去找伊拉贝思。
追问是谁获得额外经验,然后过运动检定救人,sl通过检定,让他们去找伊拉贝思。
返回下楼梯,继续往左上方向走,接到救伯爵的任务,继续走,在神殿门口过剧情并发现拉米恩,对话,接凝视星辰任务。旁边捡到虎虎,给兰恩。
 目前经验12682/15000,buff剩余时间不到一分半(如果经验不够,注意看地图中的技能检定是不是都过了)
目前经验12682/15000,buff剩余时间不到一分半(如果经验不够,注意看地图中的技能检定是不是都过了)
再往右走的一群敌人里虫裂魔最麻烦,应对方式有两种:1 席拉或者其他能t住的角色迅速冲到它面前,它就不会放aoe了;2 我放油腻术控了(它反射6,主角的油腻术豁免难度18),然后沃尔吉夫冲锋过去两轮杀了
 旁边的房子之后再来,因为需要用到防死结界卷轴,目前还没买。
旁边的房子之后再来,因为需要用到防死结界卷轴,目前还没买。
继续往前,遇到柯尔,对话推进席拉任务。对话结束后如果buff时间结束了就可以收工捡捡东西去找小烬了,如果buff还在可以再往前打一群食尸鬼,打完就不要再往前了,后面同样需要防死结界 
路上德斯娜神殿右侧的这个地方的怪也没有打,因为敌方法师会燃烧之弧,最好还是用上共用抵抗火焰再来,里面还有一只暴怖魔,对现在的我们来说也比较难 
返回,到胡尔伦这里时对话说拉米恩不是你的敌人,获得经验。接下来的对话自己选,我打算杀死胡尔伦,所以没有选让胡尔伦去铁卫雄心的选项、也没有回去把胡尔伦的决定告诉拉米恩。如果不打算杀胡尔伦,也完全可以让他去铁卫雄心、把胡尔伦的决定告诉拉米恩后看拉米恩离开。
杀胡尔伦:直接对话选择攻击,席拉t住,沃尔吉夫和兰恩第一轮杀死旁边的两个小兵,主角放油腻术控住胡尔伦(他反射6),山茶给胡尔伦上邪眼降ac。这次渐隐术不是很有用,因为胡尔伦的措手不及ac只比常态ac低一点,不如放魔法飞弹补刀。打死获得+1半身甲和公正长剑(给席拉换上),回去找拉米恩,告诉他胡尔伦死了获得636经验,再让他去找伊拉贝思。目前经验14788/15000
回到这个地方和凯丽莎对话,过世界和察觉检定,放她走。结束对话后全员升级

烬入队+升5级
去小烬那边,入队前记得关闭仅活跃队友获得经验,今后不用再打开了
全队升级
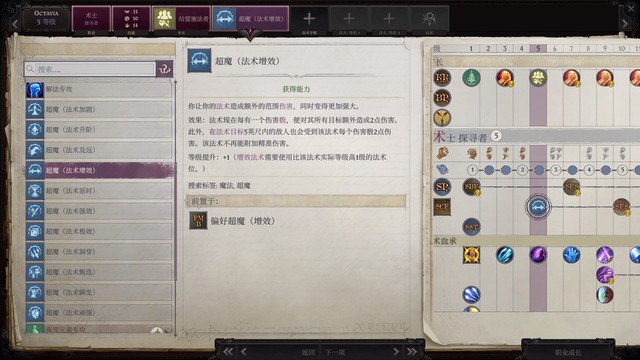
主角:法术穿透(结盟施法者被改了,废了),超魔(增效)(如图,很适合用来提升魔法飞弹的伤害),克敌机先,鹰之威仪
席拉:包抄,救赎-疲劳
山茶:优雅刺击-细剑
兰恩:包抄,终势斩
沃尔吉夫:擅长盔甲(轻型)(当时是为了之后点神话轻甲强攻,但后来神话轻甲bug修了……),狐之狡黠、识破命门
小烬:
4级,魅力,神秘、宗教、使用魔法装置,邪眼(可以和山茶的叠加),凛冬之握(酒馆保卫战用
5级,多的技能点还是点了宗教,法术穿透,凶兆,骨拳术
市集广场第一次探索收尾+聂纽入队+黑翼图书馆
给席拉换上烈火重型硬头锤,进小烬旁边的房间,主要靠席拉和小烬的燃烧之手输出。如果兰恩刚好能对集群造成恐惧也挺不错的。打完发现一个召唤法阵,先不碰它,出来。目前经验15168
如果同伴身上有打鼠集群留下的腐热症,可以让烬用属性栏的【治疗负向效果】解除
然后就可以出地图了,广场那边的集群下次再来打。出来之前把不需要的装备扔地上,下次再来捡,最好保持在中载及以下。
出门向黑翼图书馆方向出发,触发随机遭遇,进地图后用药水上缩小、变巨、防护邪恶buff
和聂纽对话通过检定获得额外经验,在整个地图仔细逛逛,注意察觉检定是否全都通过了,最重要的是捡到损害长剑(可以卖钱,没杀胡尔伦获得公正长剑的话,也可以让席拉拿这个做武器)。目前经验15523
聂纽用卷轴学猫之轻灵(沃尔吉夫上次休息做的)、油腻术、英雄气概和朦胧术(序章买的)
聂纽升级
4级,智力,隐匿、神秘、世界、使用魔法装置,召石、狐之狡黠(比召石更优先的是闪光尘,只是因为主角已经学了闪光尘了)
5级,多的技能点点了隐匿,高等法术穿透,移位术、高等魔化武器(加速术之后买卷轴学)
黑翼图书馆
服从本能解锁诡计大师道途。
搜刮,“值得注意”分类下的书都用主角读一遍,可以提供加值。获得威压木棍、魔法精华,通过所有检定。救圣教军,和说书人对话,送他回铁卫雄心。
如果买了dlc4可以看到狮鹫雕像飞了
回铁卫雄心休整
席拉剧情结束后卖垃圾(不确定能不能卖的可以卖给沃尔吉夫,方便回购),我卖了诱捕长弓、安息之恩、次等念力之冠、寒铁精制品长剑和重型硬头锤(带烈火二字的还是留着)、+1革甲、一件+1半身甲(共3件,一件席拉穿了,一件留着(可能可以给索希尔用),一件卖),造成x伤的卷轴/药水也都卖了,看过的书也卖了
黑翼图书馆获得的缩小术卷轴给聂纽学了(之后再做卷轴给沃尔吉夫学),主角不需要威压木棍的话就给聂纽拿着
和新出现的npc聊天,能交的任务都交了。完成后经验17409
如果买了dlc4,出酒馆门再进来之后触发新队友入队剧情。鸟哥升级:运动、自然、察觉、使用魔法装置,包抄。他身上自带+2力量腰带,可以扒下来给席拉穿,披风和戒指我给沃尔吉夫了
购物
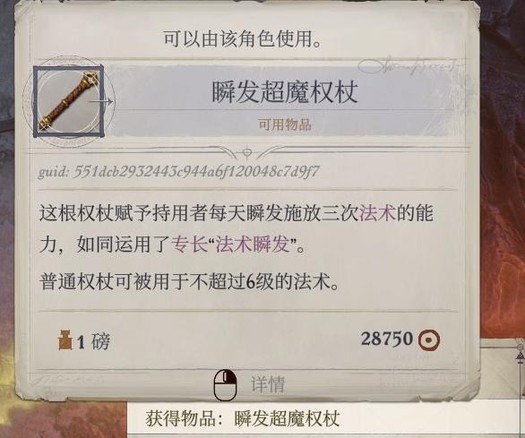
牧师:低等延时超魔权杖、共用防护火焰(市集广场某房子用)、防死结界+复原术+行动自如(可以多买几张,这三种都是多备一些总比日后没有好,我各买了三张)
酒馆老板:小型次元袋、祝福武器药水*5
沃尔吉夫:加速术(给聂纽学了)
剩下的如果钱不够也可以以后再买:共用防护酸蚀(黄玉必应屋用)、黑暗罩纱、初学者手套(给主角放魔法飞弹用,没需要可以不买)、黑暗预兆(给术士主角扩表用,没需要可以不买)、共用抵抗火焰、共用防护火焰(这两张后面打灰兵营用)
在酒馆休息一下再去岱兰家,不然腐化涨太快了
休息前改法术
山茶:一环二环不用动,三环改成共用抵抗能量、共用延缓毒发
沃尔吉夫:法师护甲2(因为不确定从岱兰家到山茶家之后法师护甲buff会不会掉,应该不会,但还是保险起见……如果没掉就分一个给兰恩吧)护盾术2七彩喷射1,猫之轻灵2识破命门1
聂纽:渐隐术2变巨1缩小2法师护甲1(在山茶家给席拉上,因为敌人会粉碎盔甲),朦胧术1狐2次元陷坑1,移位2加速1
休息时让聂纽做缩小术卷轴,休息完给沃尔吉夫学
低等延时超魔权杖给聂纽,之后在格温姆宅邸有用
出门,这次带的队是 主角 席拉 兰恩 柯米丽雅 沃尔吉夫 聂纽,去岱兰家
岱兰家和格温姆宅邸
现在起的常规buff
席拉:防护邪恶/虔诚护盾,缩小,树肤,移位术。打精英怪的时候还可以再来个鹰之威仪,提升辟邪斩效果
兰恩:牛之蛮力,变巨,诱变剂(力量),有难打的用极意击
沃尔吉夫:猫之轻灵,缩小,法师护甲,护盾术,有难打的敌人再上识破命门
全员:祝福术、加速术
共用抵抗能量/共用防护能量/共用延缓毒发都根据敌人配置来上。英雄气概也是好东西,但聂纽法术位不够,就先不记了。
下面的看情况上,都主要是用来提升法术豁免难度的:
主角:鹰
聂纽:狐
山茶:枭
岱兰家
此处还要上共用延缓毒发和共用抵抗火焰。兰恩的诱变剂这次先留着,到山茶家再用。加速术也可以先不上,真难打的话用了也行,到山茶家用奥法契约恢复。给聂纽的延时法杖也先不要激活。
凶猛速袭魔可以让聂纽用致盲射线目盲(但我roll穿透法抗只roll了5,没穿透,我让主角用刺耳尖啸控了),渐隐术对它无效因为它有识破隐形,不如用魔法飞弹补伤害。其他怪有了延缓毒发+抵抗火焰就都不成威胁。
打完和岱兰对话,问他要感激,获得戒指可以卖钱。先不带他。和阿兰卡对话,推进凝视星辰任务
格温姆宅邸
出岱兰家,去格温姆宅邸,一楼敌人密度没那么高,可以看见恶魔之后再开始上buff(树肤用魂契物恢复),兰恩用诱变剂、席拉用法师护甲(因为敌人会击破盔甲),聂纽用延时权杖给席拉上延时移位术和加速术。
一路尽快打,东西都别捡,争取最大化利用buff持续时间。
图书室的咒法师会隐形,开战时记住ta的位置,主角往那边放一个闪光尘。如果抢到了先攻并且队里有远程输出可以先打他。
二楼有杀手的房间,杀手的攻击加值比较高,难处理的话可以交一个控制法术(我这边是主角用魔法飞弹补伤害,趁他打出来之前收人头了)
到二楼最后一个房间前,我的加速术移位术buff都掉了。聂纽用奥法契约回复一个加速术,再上一次。里面的7级暴怖魔最难处理,主角的油腻术和闪光尘、山茶的凛冬之握、聂纽的次元陷坑都可以上,有什么用什么
全打完之后叫格温姆上来,过剧情,结束后捡东西离开。注意杀手房间需要过察觉,可以捡到移位术、移除疾病和石肤卷轴,捡的镰刀之后也可以卖了  目前经验19220
目前经验19220
第二次去市集广场
进门先把不需要的装备丢地上,保持轻载,免得拉慢移动速度。先不用休息,也不用上buff
灵使任务
喝药水(席拉虔诚护盾+缩小术,兰恩变巨),找门口那条路上唯一戴着头盔的圣教军,发现他是德斯娜牧师,支持他,和审判官开战。
结束后去德斯娜神殿,跟着唱歌解锁灵使道途,再出神殿休息。
休息
沃尔吉夫的一环法术改成1法师护甲2护盾术2缩小术
聂纽的法师护甲也可以改(我改了七彩喷射
其他法术都没必要改,沃尔吉夫做一张克敌机先给聂纽学
目前除了市集广场之外,触发酒馆保卫战之前需要探索的地方都已经去过了。在市集广场内部也不可能触发酒馆保卫战,所以现在起可以需要休息就休息,把市集广场打完再离开地图(出去的时候最好还是不要带太多东西,可以优先带 价格/重量比 更高的),离开后可能在半路触发信使来让主角支援酒馆保卫战。
市集广场上剩下的地方怎么打:
妄乱魔
回到遇到小烬旁边的房间,完成召唤法阵。再去之前遇到胡尔伦的地方的右上方,出现了妄乱魔。上满buff(除了祝福术,可以等妄乱魔给队友上了孢子再上),席拉上辟邪斩,主角给兰恩渐隐术,山茶上邪眼,砍它。
遁影魔
打完妄乱魔之后捡到旁边的秘银重盾,给席拉装备。走旁边的灵巧检定,来到之前说先不用进的房间门外。里面的地下室里是隐形的遁影魔,给席拉用抵抗寒冷药水(序章捡的)和石肤卷轴,菲尼安变新月战斧给兰恩(菲尼安可以对虚体打满伤害),主角用天使之光把敌人照出来,然后再用闪光尘取消敌人的隐蔽,山茶还是复读邪眼。
不死生物
打死之后先不捡东西直接出门,趁buff时间还没结束,去打右上角的怪,到达的时候给席拉补一张防死结界卷轴。
第二群僵尸(p1位置)打完之后,先不急着朝p2的右上角走,过去就要打成就怪了。

邪教徒死灵师
给兰恩换回恐惧进击,聂纽给大家上加速术,移位术也可以用了(不一定给席拉,席拉能顶住,反而是兰恩/主角可能成为敌人的另一个目标),开局如果三个近战先攻roll得高可以冲锋过去,还可以用凛冬之握/油腻术控一下
打完之后我的buff刚好也掉没了,搜刮一下一路上的物资
其他杂兵
然后不带buff把旁边这里打了(需要共用延缓毒发),还是比较轻松的,顺便救剧团

然后去收拾德斯娜神殿右边的怪,山茶给共用抵抗火焰,其他buff不是很有必要,看着上吧,打完几个邪教徒和深处的暴怖魔。如果上了buff就尽量快点赶路到地图左下(目前只剩大地图左下没有去过了,从下图中这个地方过去  过去之后往前走,看到敌人再开始上buff,对速袭魔依旧可以用致盲射线,对会隐形的法师依旧用闪光尘,有两个速袭魔的地方 凛冬之握/油腻术/刺耳尖啸之类的控制法术也可以交一下
过去之后往前走,看到敌人再开始上buff,对速袭魔依旧可以用致盲射线,对会隐形的法师依旧用闪光尘,有两个速袭魔的地方 凛冬之握/油腻术/刺耳尖啸之类的控制法术也可以交一下
直线路径上的敌人杀光之后马上转身上楼打上面的敌人,我的buff时间还剩两分半
进着火的房子之前记得上共用防护火焰。打完搜刮(最重要的是拿到圣徽碎片,骤然巨力也可以给席拉装上),整个地图应该就只剩遇到胡尔伦的地点上方的集群没打了,其实可以休息一下再打,但我实在不喜欢打集群,不打了……!
休息一下再离开地图(离开之前记得和地图左下角靠中间位置的混种人对话)(休息时让聂纽做镜影术给沃尔吉夫学)目前经验21731
回铁卫雄心休整
提前休息是为了防止回酒馆的路上遇到通知酒馆保卫战的信使。
酒馆保卫战前置随机遭遇
这场战斗的主要难点是开始时队伍是无buff的状态,所以需要抢到先攻上buff。有什么法术和能力资源都可以交了,反正回到酒馆还可以再休息。我这里用到的比较重要的技能是共用延缓毒发和次元陷坑。
回到酒馆,卖垃圾,飞斧、镰刀、短弓、短矛、戮军斧、+1胸甲也都卖了,目前16932金币。上次说可以之后再买的东西里,共用防酸和初学者手套我买过了,现在又买了共用抵抗火焰、共用防护火焰、黑暗预兆(直接给主角戴上了)。想买的东西里只剩黑暗罩纱没买了
岱兰升级:
4级:魅力,宗教、沟通、世界;音鸣爆(打灰兵营用
5级:专长:技能专攻-宗教(因为带岱兰的时候多半不带索希尔,没人过宗教),绝不动摇、牛之蛮力
战前准备
酒馆保卫战队友:席拉 兰恩 柯米丽雅 小烬 聂纽。休息前法术改一下,之前记的是双份buff,这次每等级一分钟的buff可以改成只记一份了,多出来的法术位可以记增伤/控制类法术(比较好用的群体法术:凛冬之握、致病纠缠)。
酒馆保卫战开始时队友身上是没有buff的,需要在战斗内上。有个小技巧是算好每个队友需要的上buff的回合数,尽量平衡各个队友上buff的回合,比如如果柯米丽雅需要上的buff太多,就可以看看能不能让其他队友分担一些/用药水解决,因为回合制下基本是上完buff才能离开门口就位加入战斗
改好之后存个档,睡一觉,醒来就是保卫战了
酒馆保卫战+升6级
(没打算做保护酒馆不受毁坏的成就,不公平难度做这个太难了)
回合制的酒馆保卫战是真的又臭又长……开局先站原地把buff上了,加速术移位术先不用上,烬需要上的buff不多,可以最先在p1图中右侧道路上放凛冬之握控敌人(最好在下方侧边留出一条小道让变巨兰恩能站过去打到敌人而自己不被控),山茶的致病纠缠也可以放这里,席拉可以到p2楼梯的位置顶着,其他人找个地方待机、补补伤害就好了(最好是p1p2两处都能兼顾到的),法术最好先留着少用,烬闲着没事就上邪眼/易伤/沉眠吧
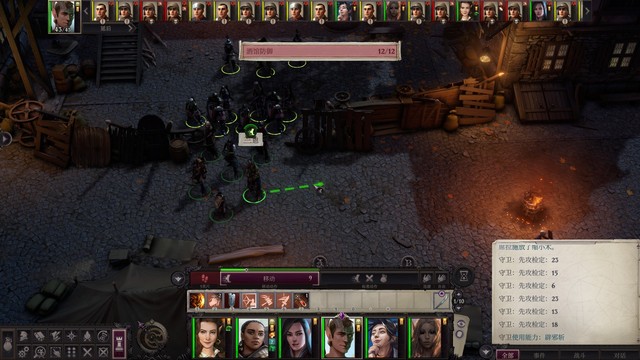
就位之后差不多就这么个情况,兰恩在两头跑来跑去打
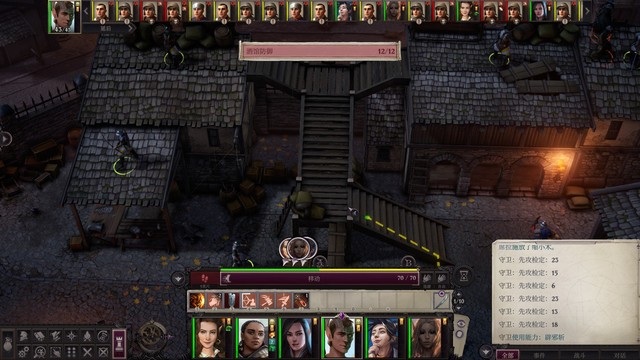
打一阵子之后出现第二段动画,屋顶上的敌人增多而且更强,可以让兰恩站过去重点杀一杀(另一侧继续让小烬/山茶控着就行了),主打的就是快进到第三阶段。席拉那边顶的敌人多起来之后就可以考虑让聂纽上延时加速术了。 
(初信者战士是无限刷新的小怪,应该不影响战斗进程,想推进战斗需要杀死其他名字的敌人)
进第三阶段之后的走位就更多靠随机应变了,我是席拉兰恩打牛头人,山茶打新出现的赘行魔,聂纽控新出现的炼金术士,主角小烬支援。延时移位术可以上给席拉了,加速术没了也可以补,辟邪斩、法术也都可以放了……只要打到这里不是弹尽粮绝,应该不难过,牛头人ac还不如速袭魔呢。
(在快打完的时候让没事干的队友去捡战场上的装备,之后卖)
打完就升6级了,如果dlc2已通关,额外获得一个权杖。 
6级
主角:臭云术(没必要学火球术,第二章可以买炽热火蛇戒指
席拉:同以前一样
山茶:同
兰恩:血怒者-原怒者(后面神话1拿无限狂暴),天界
沃尔吉夫:蛛网术(让他和聂纽互相做卷轴补充法术书),牛之蛮力
烬:尖笑、毒液啐沫
聂纽:火球术、共用防护箭矢(抄成卷轴用)
岱兰:操纵亡者
鸟哥:同
到酒馆室外可以领到战利品,还有伊拉贝思给的武器,没什么大用,也可以直接卖掉(但dlc2权杖还是先留着比较好)。然后就有钱买黑暗罩纱了,购入!
之后第一章就没有时间限制了,可以慢慢打。
聂纽的三环法术位还可以记英雄气概(但我图方便记双份buff,所以还是加速术2移位术2)。
给山茶记了个鹰之威仪,打boss的时候给席拉上,三环多的法术位就记操纵亡者。
席拉的圣武士法术位记了天堂面纱。
休息一次之后出门去市集广场(队伍:席拉 兰恩 山茶 聂纽 沃尔吉夫),这次休息让聂纽做朦胧术给沃尔吉夫学
第一章小地图收尾
市集广场
酒馆保卫战后市集广场出现了新的怪,位置比较分散,多逛逛,看到敌人再上buff就好。
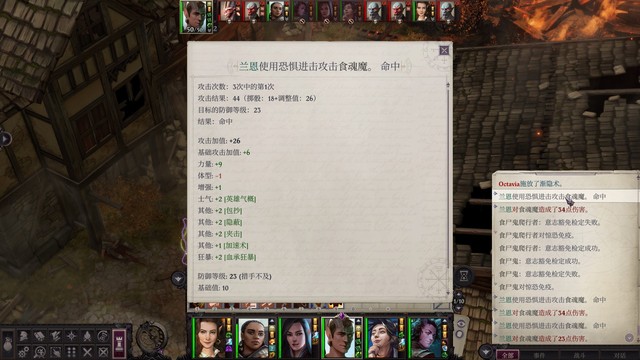
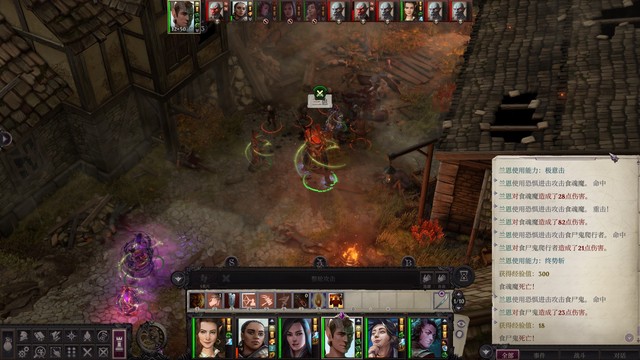
主要目标是打食魂魔获得成就教长代行者,出现在之前死灵法师的位置,走近触发,满buff,如果聂纽还可以给兰恩上英雄气概。给席拉防死结界、鹰之威仪,席拉兰恩行动自如+祝福武器药水,席拉过去触发战斗,没有防死结界的队友可以在远处待着,有加速术+狂暴+祝福武器+渐隐术+满buff的兰恩砍两三轮就把boss砍死了。打完经验23712
 然后随便逛逛清清怪就走了。
然后随便逛逛清清怪就走了。
这次出去捡上所有东西回酒馆卖掉。目前经验23874,吞噬护符、损害长剑和+1链甲也卖了,我又卖了2级做卷轴工具,购入了3级的,为了让聂纽做共用防护箭矢(能在灰兵营硬顶一下集群伤害)。
再休息,法术位不用动,聂纽做一张【共用防护箭矢】留着(或者沃尔吉夫做蛛网术给聂纽学),再找牧师购入一些防死结界和行动自如卷轴备用。
去皮塔克斯的酒窖,进门满buff开战,打完房间内侧过察觉捡到武器,可以卖。
去黄玉必应屋,上共用防酸,满buff,打完拿到先知之祸轻弩和菜谱
去提拉巴德的住处,进去之前休息一下,把山茶的一个二环法术位变成【共用防护阵营】,接下来打魅魔的时候用。聂纽还是做共用防护箭矢。
进地图先上除了加速术移位术之外的buff,先打街上的敌人(这里难打的话可以在虫裂魔现身之后在它身边放一个操纵亡者),打完进门,山茶隐匿过去解除陷阱再回来,上共用防护邪恶、加速术、移位术,给席拉上防死结界,开战,法术/能力都可以用了,对魅魔用闪光尘,然后给兰恩续渐隐术打措手不及(它常态ac40,措手不及ac30,兰恩攻击加值26),山茶就复读避灾/邪眼,打完就可以捡捡东西回酒馆了。
第一章小地图全部探索完毕,准备去灰兵营
卖东西清理背包,斧头、木棒、公正长剑我都卖了,需要的话还可以再买点卷轴药水什么的,我以防万一又买了一张共用防火。
buff记双份,聂纽不用记加速术,换移位术
再做一张【召石】卷轴留着,食物吃加移动速度的,队伍配置沃尔吉夫换成岱兰
灰兵营+神话1
进灰兵营获得加速术buff,其他buff先别上,这一层的东西捡完之后上每等级10分钟或1小时的buff,以及共用延缓毒发、共用抵抗火焰,还可以给主角挂个渐隐术(上楼敌人仇恨可能在主角身上),然后上楼。
岱兰和主角可以复读打击士气,打完没必要浪费时间捡东西,之后还会回来。再上一层楼,如果有德斯娜牧师帮助,他们会让虫裂魔沉睡,看完动画过去让兰恩对虫裂魔使用致命一击就好,打完再上每等级一分钟的buff
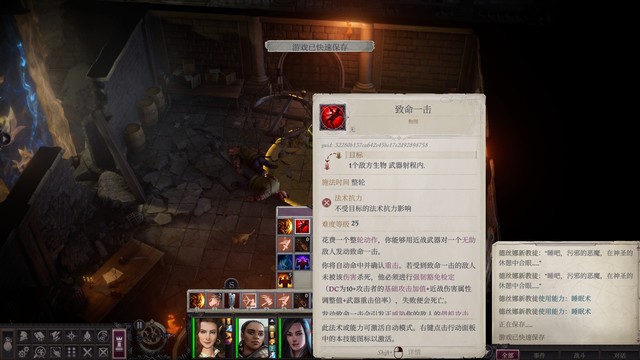
- 接下来会尽量走最快速到达boss门口的路,其他非必经之路上的小怪可以打完boss拿到神话1再来
往前走,打完外面走廊的小怪,再次下楼前往一楼,这是我们之前序章走过的地方。打完门口小怪和魔法门互动,圣教军法师会帮忙开门,等待开门后杀门后走廊上的小怪。
然后使用共用防火卷轴,再开图示房间的门,开门时会自动存档,打不过的话读档,敌人就会恢复到没有发现主角队的状态,可以在这种状态下做其他准备。
 至于打法,我用了闪光尘+臭云术,兰恩砍中了再恐惧几个,就好处理了。打完察觉到房间右上的暗门(如图)
至于打法,我用了闪光尘+臭云术,兰恩砍中了再恐惧几个,就好处理了。打完察觉到房间右上的暗门(如图) 
上楼,开门前给主角上渐隐术,开门开战。打完出门遇到暴怖魔,再打完,走到p2p3所示门前,开门之前给席拉上个移位术,席拉开门开战。
 在这里主角又扔了臭云术,岱兰用了操纵亡者(不用太节省,打boss之前会贴心地回复所有法术位的)。我打完这里的时候每等级一分钟的buff差不多要掉了,捡捡东西休息一下,这次记得休息前记加速术(捡到一个+2敏捷腰带可以给兰恩,+2巨力腰带和骤然巨力可以给席拉)。
在这里主角又扔了臭云术,岱兰用了操纵亡者(不用太节省,打boss之前会贴心地回复所有法术位的)。我打完这里的时候每等级一分钟的buff差不多要掉了,捡捡东西休息一下,这次记得休息前记加速术(捡到一个+2敏捷腰带可以给兰恩,+2巨力腰带和骤然巨力可以给席拉)。
这一层楼目前只剩三个速袭魔和一个小boss区域了,速袭魔中的两个会被德丝娜牧师催眠,剩下一个无buff也能打,然后就只剩图中这扇门后面的小boss没有打,到门口再上第二轮buff。

 满buff,给席拉法师护甲,用上黑暗罩纱,开门。
如果有dlc2:第一轮用夺命暴雪权杖对boss上魔法飞弹,造成缓慢术效果,让她放不出虫群。席拉兰恩集火boss尽快杀掉。
如果没有dlc2:用防护箭矢抵消集群伤害,同样集火boss。
满buff,给席拉法师护甲,用上黑暗罩纱,开门。
如果有dlc2:第一轮用夺命暴雪权杖对boss上魔法飞弹,造成缓慢术效果,让她放不出虫群。席拉兰恩集火boss尽快杀掉。
如果没有dlc2:用防护箭矢抵消集群伤害,同样集火boss。

打死之后获得钥匙,去开需要钥匙的门。打完丧尸继续前进触发冥娜蛊斯陶顿剧情,看完上楼遇到强力牛头人,ab29,兰恩用祝福武器药水,席拉上辟邪斩,抢在它之前用召石卷轴造成困难地形让它无法冲锋,我还用主角给它上了衰弱射线、聂纽上致盲射线、岱兰打击士气,它的ab就被降低到20了,兰恩迅速击杀。
这之后就是boss战,进战斗自动回复所有法术位并且获得如图龙傲天buff。
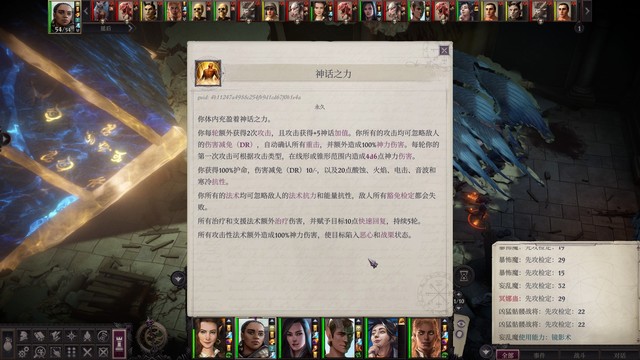 一开始不要走得离冥娜蛊太近不然她会传送走,在龙傲天buff下我们的法术dc会非常高,所以可以先用法术控住她(主要目的是让她不要放出来腐烂幻象)。打到一定程度之后出现第二波小怪,这波小怪的初始仇恨在主角身上,很烦,也可以提前铺一些地形法术控住,优先集火冥娜蛊,把冥娜蛊血条打空触发剧情之后怪就都走了
一开始不要走得离冥娜蛊太近不然她会传送走,在龙傲天buff下我们的法术dc会非常高,所以可以先用法术控住她(主要目的是让她不要放出来腐烂幻象)。打到一定程度之后出现第二波小怪,这波小怪的初始仇恨在主角身上,很烦,也可以提前铺一些地形法术控住,优先集火冥娜蛊,把冥娜蛊血条打空触发剧情之后怪就都走了
神话1
主角:打算走灵使所以选无拘乐器,偏好超魔-增效(之前超魔到二环的魔法飞弹也没删,之后一环二环都可以放增效魔法飞弹了
席拉:屹立不倒
柯米丽雅:屹立不倒(2026更新:当前版本(大概率也是最终版本)的柯米丽雅近战不是很强,玩法术可以选腐秽侵世)
兰恩:无限狂暴
聂纽:充裕施法
岱兰:第二秘示域-自然
沃尔吉夫:变化自如
烬:巅峰元素-火
鸟哥:变化自如
索希尔:领域痴迷
然后下楼去探索之前没去的地方。如果中了冥娜蛊的力竭波,可以让席拉用圣疗解除
图中这个陷阱手动解除(而不是让魔裔解除)给960经验,如果巧手不足就用那个可以暂时提升技能点的家族徽章道具

彻底打完捡完东西就走了,超重的话把东西丢在地上,出地图时会弹出窗口问要不要带上战利品,这时再全带上就好。目前经验/负重/金币是这么个情况。出灰兵营进第二章了!
第二章
进入新章+升7级
成为指挥官!找说书人对话,修复后继者圣契,好东西,务必随身携带,不要交给女王(虽然交了有经验)(当然低难度就无所谓了
进指挥官帐篷之前在其他地方都逛一逛,对话、搜刮。进指挥官帐篷触发剧情之后外面的垃圾会更新,可以再搜刮一次。如果想攻略女王,这里可以选择说服女王参加圣战。如果想做虫群道途,就最好不要让女王加入了,不然后面她会阻止我们做虫群道途的邪恶选项。
有后继者圣契之后不再需要寒铁武器了,给山茶换成+1细剑;闪耀匕首给沃尔吉夫,替换原本的寒铁匕首;生机半身甲先给席拉穿了。卖完不需要的装备之后背包是这样,金币43527。


 黑暗之角先给索希尔拿着了,黑镜护符给了小烬
黑暗之角先给索希尔拿着了,黑镜护符给了小烬
和所有能对话的npc对话之后我的经验是34972/35000(正常情况下如果前面没有漏经验,应该已经7级了),距离升级只差一点点,所以我在出门之前走了走圣教军棋(雇佣法师将领【市刹那】,兵优先买射手),完成了几步圣教军任务之后就升到7级了。
7级
主角:高等法术专攻(塑能),精通先攻,护盾术,镜影术(一会儿在索希尔墓园就可以用这个保命),英雄气概,
席拉:盔甲专攻(中甲),武器神圣盟誓
兰恩:擅长异种武器-斩矛,长柄
聂纽:超魔-延时,高等隐形术,冰风暴(后面麻风病人的笑容用)
岱兰:法术专攻-塑能,动物伙伴-狼,魔化武器(其实不知道点什么了……),鹰,神使灵光
狼:蛮力,灵巧、使用魔法装置,欲魔落袭,武器专攻,力量,闪避,7级专长是包抄,买到书呆子头带给狼戴上再升级点包抄
索希尔:3灵巧,精通先攻
柯米丽雅:包抄
沃尔吉夫:包抄,磨锋砺刃、高等魔化武器(聂纽也会,但聂纽目前法术位比较缺,分担一下),用卷轴学了移位术(格温姆宅邸过察觉拿到的)、共用抵抗能量(第一章买的 没用到)、共用防护箭矢(聂纽做的)
小烬:超魔(增效/加剧),变巨/雪球术(随便选的),蛛网术/闪光尘,英雄气概(在有主角和聂纽的情况下不太会再带烬了,所以点得挺随便的)
乌布里格:突刺
第二章可以买的好东西
越早买越好:
低等延时超魔权杖
碎虫者(给兰恩前期拿着用用
无阻法袍(现在没了结盟施法者,感觉更重要了……
到麻风病人的笑容之前买:
书呆子头带
救地狱骑士之前买:两张群体次元门卷轴(用来逃课)
买完上述物品后还有钱就买:
低等强效超魔权杖
自然的惊愕
迫降护腕
次级决斗手套
炽焰火蛇
霜护(可以给柯米丽雅)(如果玩远程就不用了)
骗徒戒指
莎恩芮战裙
6级卷轴制作装置+腐烂幻象卷轴(=可以让聂纽做更多腐烂幻象卷轴为眷泽城做准备了)
另外其他好用的还没学的法术对应的卷轴也都可以买来给聂纽学
索希尔任务
出门之前先给升过级的队友记法术,之前没提到的常用buff:
索希尔:骨拳术、共用延缓毒发、抵抗能量、神使灵光、圣战之刃
席拉:圣能面纱
聂纽:高等隐形术(虽然学了超魔延时但第二章前期还用不到,四环法术位比较紧缺,等神话2拿到偏好超魔或者精通充裕施法就舒服多了)
记完所有要用的buff之后,多余的法术位多记控制类法术,保证打强韧/反射/意志的三类都有
休息一下,沃尔吉夫这次可以做蛛网术给聂纽学了,或者聂纽做三环法术提前帮沃尔吉夫备着
索希尔任务地图
配队:席拉 兰恩 聂纽 索希尔 岱兰(有神话1之后岱兰可以替柯米丽雅上树肤了,所以可以把她换下来。岱兰还有狼,还能用引导能量打丧尸,在高难度的索希尔任务地图里比柯米丽雅更强。低难度还是推荐柯米丽雅或者沃尔吉夫,因为他们会开锁,地图里有宝箱)
进索希尔任务地图看完剧情就是战斗,无buff情况下回合制太难了所以我先切了即时,除了席拉之外的所有人往画面右侧跑,席拉殿后t住,眼看跑不掉了再切回回合制,主角给自己上渐隐术然后上油腻术控敌人,聂纽先上加速术和移位术再上别的buff,岱兰和索希尔看情况决定是加血还是引导能量伤害不死生物。第二波敌人出来之后初始仇恨又在主角身上,给主角上隐形术,席拉T住
现在兰恩有无限狂暴了,记得进战斗看一眼狂暴开了没,没开的话手动打开。高等隐形术当作渐隐术的上位替代就行。后面的战斗没什么难的,整个地图打完经验38672
回去休整
回军营卖垃圾、休息,军需官处购入自然的惊愕给席拉穿,因为自然的惊愕限定的最大敏捷加值是3(原本生机半身甲是0),今后聂纽可以给席拉上猫之轻灵提升ac了(没有就穿+2敏捷腰带)。换下来的生机半身甲给索希尔穿了。
我之前选择让女王参加圣战了,这次回来看到女王加入营地,对话获得400经验
席拉任务+夜莺林+未解之谜+回营地
今后的常规配队:席拉 兰恩 聂纽 小贼 岱兰,buff都是能记双份就记双份的
猎心营地
进席拉任务地图,过剧情、捡东西,左边能捡到好盾牌,给席拉换上。触发追恶魔剧情之后再上满buff,主角上镜影术渐隐术法师护甲护盾术保命。打完就可以离开了,接下来去夜莺林。此时圣教军棋是这样。
夜莺林
主角队去夜莺林的路上会遇到事件,看到图中场景就提前上buff再靠近npc,还可以用一下黑暗罩纱。打完捡东西,有些角落要过察觉。到夜莺林门口如果没buff了就休息一下(让沃尔吉夫记一个共用抵抗能量)

到夜莺林,可以用黑暗罩纱+共用抵抗火焰,满buff(只有一次的buff也都可以用在这里,下一次休息前已经没有战斗需要打了),还可以让聂纽多给主角一个移位术保命。
未解之谜
未解之谜没有怪,逛逛捡捡东西,做完解谜拿了奖励再出来就好。我这里捡上东西之后超重了,给队友上了变巨和牛之蛮力就好了。回军营卖垃圾
圣教军棋目前打到这样,给的心灵暴政也可以卖
回营剧情+休整
回营地,触发剧情,答应去救地狱骑士
如果有联动dlc,还会解锁任务:奇怪的访客。和地狱骑士在同一个方向。
帐篷外触发小烬事件
和席拉对话(在席拉任务多选善良选项,后期席拉可以获得特殊能力)
在希洛处看到神秘的精灵
和军需官对话看到新的对话选项,我选了第二个
卖锤子、心灵暴政、链甲衫、坐骑甲、鼓舞颂歌帽、恐惧进击、审判重弩、灵巧之拳
买次元术卷轴*2、书呆子头带、次级决斗手套(给兰恩)
给岱兰的狼装备书呆子头带,升7级,点包抄,然后再卸掉。接下来可以先给聂纽戴一会儿
月舞草原+寒溪村+救地狱骑士+回营地
去月舞草原。满buff(只有一次的buff也可以用在这里),席拉靠屹立不倒扛着,效果结束的时候正好打完
 圣教军现在是这样。去寒溪村,搜刮一圈,地图右边的动物可以打一打,和月舞草原差不多
圣教军现在是这样。去寒溪村,搜刮一圈,地图右边的动物可以打一打,和月舞草原差不多
触发随机遭遇遇到了商人,买了可控火球术卷轴(非必要),给聂纽学了(还买了点复原术卷轴备用
回军营,自己的帐篷,看到神秘精灵,放她走。接下来去地狱骑士那边逃课!圣教军现在只剩那个7级的没打了,暂时先不往前推进
地狱骑士处,洞穴外侧上满buff都比较好打,不说了。进入洞穴之后,看剧情,战斗开始之后所有人到左侧灵巧检定的位置站好,用群体次元门卷轴传送到右侧,等上面打完再过灵巧回去就好了。雷吉尔入队之前锁血死不了,让他打。老雷辛苦了!
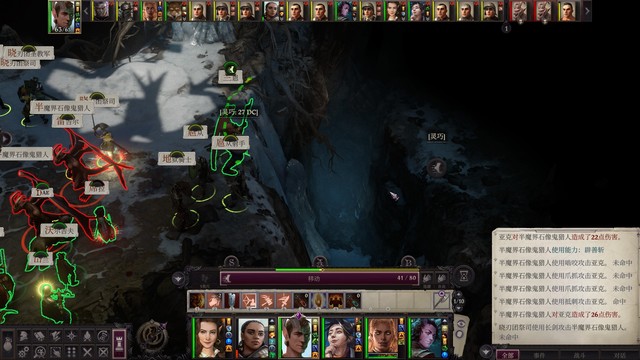
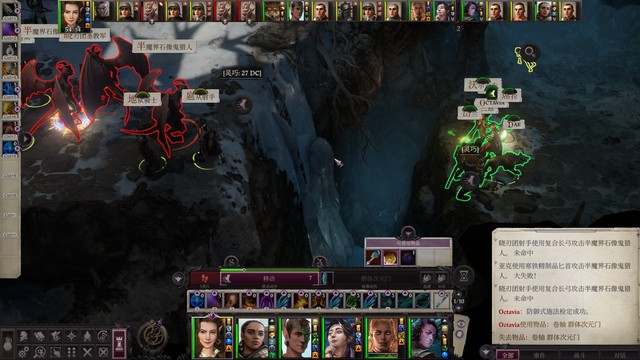 打完(老雷打完)捡到灵感头带,可以先给兰恩戴,之后带山茶的时候换给山茶
打完(老雷打完)捡到灵感头带,可以先给兰恩戴,之后带山茶的时候换给山茶
出地图,回一趟军营,把dlc4队友鸟哥自带的吊坠扒下来放背包。寄望重剑、+2胸甲和热身甲我也卖了,凑够了16200+,购入迫降护腕给兰恩。
+2防御护腕和两把长弓也卖了,凑够9000+购入了低等强效超魔权杖,之后让聂纽或者烬拿着打集群。
还要提前备上共用防护箭矢卷轴
雷吉尔我不会用,升级加点以后再看。
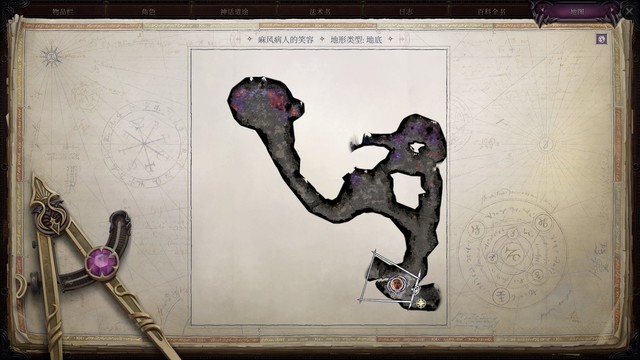
无名废墟+麻风病人的笑容地表+回营地
出门去无名废墟,还是之前的配队,探完无名废墟经验是47028。正能量经匣先不急着给岱兰戴,一会儿给索希尔在麻风病人的笑容用。
在到麻风病人的笑容之前休息一下(去的路上触发了随机事件,三个暴怖魔,打完捡到纸条,解锁不起眼的营地),我做了一张火球术卷轴(共用防护箭矢够用了
休息之前改法术,这次聂纽四环可以记两个冰风暴/可控火球术了,三环有空余位置也可以记火球术,buff记一份就好,沃尔吉夫的buff不重要反正不带他(最后其实火球术没派上多大用场,主要还是靠兰恩砍的)
到了之后选雷吉尔的方案、牺牲少数受害者,这是小队要带索希尔的情况下的最优解。
进地图,可以把小贼换成索希尔(索希尔给兰恩上圣战之刃),给兰恩装备集群克星吊坠、书呆子头带。岱兰换不换小烬无所谓,反正都用处不大,带岱兰可以看恋爱剧情(
- 安妮维亚提醒不要急着发财不然扣女王评价。这里的判定其实不是什么都不能拾取,而是不能拾取珍贵装备。可以打开拾取物品的窗口,拾取好装备后,再打开不含珍惜装备的窗口,把原先的窗口顶掉,就不会被判定为拾取了钱财。
(我主要就是拾取了轻丝袍给席拉穿,捡完就直奔虫群女王了(因为真的不爱打集群+没那么缺经验)
战斗:上了共用防护箭矢卷轴之后,只让兰恩和席拉走在最前面,其他人在远处放法术/加血,记得给席拉的武器换成打钝击的,我换了之前第一章就用过的烈火硬头锤。有dlc4送的吊坠的情况下很好打。集群免疫魔法飞弹,但王室卫兵不免疫,而且增效魔法飞弹造成的额外伤害 集群也不免疫,所以主角也可以对王室卫兵放一放增效魔法飞弹
车夫救一下,之后第四章给好东西
打完到地下看一眼,然后就出地图回去休整一下,再回来打地下
这次回营地卖了猎手确证和+1半身甲,现在身上有16000金币。休息一下然后去麻风病人的地下,buff改成双份!正能量经匣换回给岱兰了
顺便去努拉帐篷过一下察觉,发现努拉有问题
圣教军棋处获得了魔术师的戒指,给聂纽了。
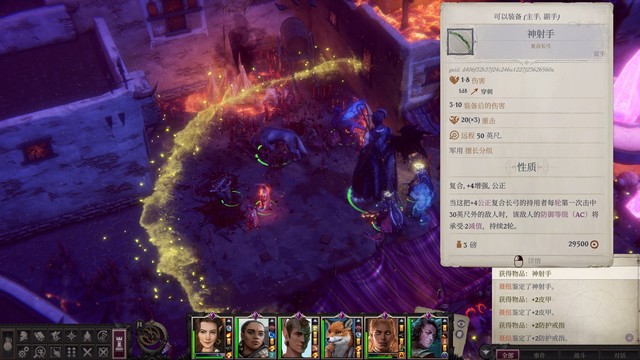
强效权杖可以换给主角了,以后可以放增效(每个伤害骰+2伤害)+强效(伤害×1.5)+天命(dlc1给的,伤害×1.1)+初学者手套(每个伤害骰+1伤害)+专精(施法者等级+2,相当于多一颗飞弹)的魔法飞弹,在现在七级放飞弹(普通情况下是4颗,每颗伤害1d4+1),一个法术的预期伤害是(1d4+1+2+1)×5×1.5×1.1=40∽65……之后还能有力场之锋(每个伤害骰+2伤害),预期伤害变成55∽80(每一颗飞弹的小数点后面的伤害都先删去了)……还是很厉害的!
麻风病人的笑容地底+8级+回营地
这次的配队是主角 席拉 兰恩 聂纽 索希尔 岱兰,忘记带巧手人了,好在地底的陷阱都是可以绕过的
现在打地下毒啮魔是这样


第一次休息之前打了这些,陷阱绕过去了,拿到了+2长剑、虚空之声和辐光反曲刀,打算都卖了。集群已经全部打完了,给席拉换回骤然巨力(换下来的武器应该也可以卖,不过我以防万一就先留着),兰恩的书呆子头带和集群吊坠也可以换了。
 不小心让岱兰被中了debuff的兰恩砍死了一次,用掉了银龙鳞片,不过之前给说书人看过鳞片了,应该不会卡任务。
前半段的buff就是常规buff,唯一要注意的只是让索希尔给兰恩上圣战之刃,获得额外附伤,打集群打得快一点;聂纽之前记的冰风暴可以换回高等隐形术了。
有四个集群埋伏的地方,可以让动物伙伴去一侧送,暂时拖住两个集群,防止大部队被集群集火aoe暴毙。
接下来休息一下就去打尸妖那条路。目前经验50198/51000,快升8级了
不小心让岱兰被中了debuff的兰恩砍死了一次,用掉了银龙鳞片,不过之前给说书人看过鳞片了,应该不会卡任务。
前半段的buff就是常规buff,唯一要注意的只是让索希尔给兰恩上圣战之刃,获得额外附伤,打集群打得快一点;聂纽之前记的冰风暴可以换回高等隐形术了。
有四个集群埋伏的地方,可以让动物伙伴去一侧送,暂时拖住两个集群,防止大部队被集群集火aoe暴毙。
接下来休息一下就去打尸妖那条路。目前经验50198/51000,快升8级了
拿到泽卡琉斯的魔杖,选择放在包里。之后主角会自动位移到魔杖处,而且会刷出新一轮小怪,注意防御。打完捡东西,在这个分叉路能获得+2虫类破敌精灵曲刃(卖),菜谱,心灵穿刺者(给山茶),银龙爪子的碎片(需要和推车互动),+2轻敏腰带,并且队伍升到8级,到这个位置准备过去打大蜘蛛
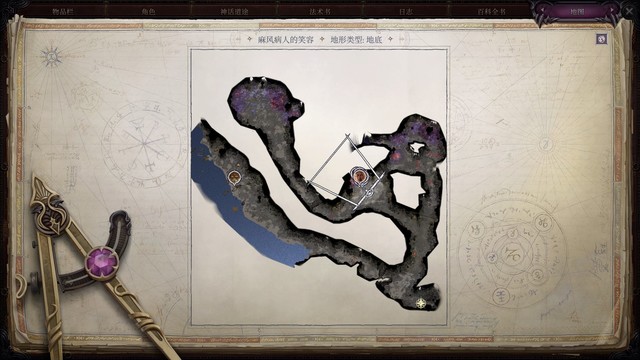 8级:
主角:魅力,咆哮术
席拉:圣武士,魅力,眩晕(随便选的)
兰恩:力量,精通重击(斩矛),菲尼安可以变斩矛给兰恩用了,碎虫者可以卖了
聂纽:智力,虹彩图纹,灭顶悲痛(感觉选得不太好,都是打意志的法术,不过主角已经学了咆哮术打强韧了,而且四环打反射的法术也不多,聂纽也学了火球术了……)
索希尔:感知
岱兰:魅力,行动自如
山茶:敏捷,冻皮
沃尔吉夫:敏捷,战斗特技-精通双武器战斗,加速术,英雄气概
烬:魅力,救难,防死结界
鸟哥:力量
狼:力量
8级:
主角:魅力,咆哮术
席拉:圣武士,魅力,眩晕(随便选的)
兰恩:力量,精通重击(斩矛),菲尼安可以变斩矛给兰恩用了,碎虫者可以卖了
聂纽:智力,虹彩图纹,灭顶悲痛(感觉选得不太好,都是打意志的法术,不过主角已经学了咆哮术打强韧了,而且四环打反射的法术也不多,聂纽也学了火球术了……)
索希尔:感知
岱兰:魅力,行动自如
山茶:敏捷,冻皮
沃尔吉夫:敏捷,战斗特技-精通双武器战斗,加速术,英雄气概
烬:魅力,救难,防死结界
鸟哥:力量
狼:力量
升级之后过运动检定过去,再重新上一遍buff,开战,它ab挺高但席拉可以用屹立不倒顶一下。战后获得搜猎仪之爪,给沃尔吉夫,药师护符我感觉没太大用处,也可以卖。打完回营地卖东西
之前买了两张次元门卷轴,在地狱骑士那边用了一张,剩下的一张给聂纽学了。
买了六级抄卷工具和腐烂幻象卷轴,早点让聂纽做起来预备眷泽城。把原本的抄卷工具卖掉,补充了一张复原术、一张防死结界。还剩14000+金币
目前第二章里想买的东西还剩这些没买:
炽焰火蛇
霜护(给山茶
骗徒戒指
不起眼的营地+地底藏身处+天堂之缘+石像鬼夜袭
收拾完出门,这次配队是老四位(主角 席拉 兰恩 聂纽)和岱兰沃尔吉夫。圣教军先往右侧推进一下,不着急攻打下一个堡垒(以防万一还需要再回去修整)
主角队去不起眼的营地,捡到精灵笔记,过察觉捡到次元门魔杖。
然后去地底藏身处打架。地底藏身处要上共用抵抗电击,抵消鬼火的伤害。鬼火的隐形用岱兰自带的闪光尘处理就好。小boss的藤蔓用行动自如解决。同仇链甲给兰恩穿,正义圣教军之戒给席拉
接着去天堂之缘,进去做完岱兰任务离开,再重新进去,就可以全队一起行动,到房间里过察觉发现德莱文的帽子(给主角,戴上就不摘了)和镜影术魔杖(石像鬼夜袭处主角和兰恩开局用过之后再给席拉)
然后就可以推进圣教军、打下一个堡垒了。需要的话也可以先回营地卖卖东西再推进。做完岱兰任务离开天堂之缘后会自动休息一次,所以不是很需要休息。沃尔吉夫身上的东西都可以卸下来了。接下来就打石像鬼。
触发石像鬼事件之后,开局只有主角和兰恩两个人,这里的buff就靠卷轴和药水上了。我是这么个情况(兰恩的法师护甲穿着同仇链甲就没必要,我上习惯了)。
 主角第二轮可以补一个渐隐术,因为第二轮石像鬼的初始仇恨在主角身上,可以提前让兰恩站在石像鬼到主角身边的路上,借机攻击蹭点伤害
主角第二轮可以补一个渐隐术,因为第二轮石像鬼的初始仇恨在主角身上,可以提前让兰恩站在石像鬼到主角身边的路上,借机攻击蹭点伤害
在努拉那边记得过察觉。可以等接到山茶和席拉入队之后再过去,会好打一点。
剩下的没什么好说的了,不难打。过了剧情就去了失陷教堂山脚下(去之前找军需官卖了垃圾,目前身上20000+金币,具体数值忘了)
失陷教堂+灰莓村+9级
之前石像鬼夜袭时用掉的法术位并不会恢复,不过没关系,buff机聂纽马上就入队。如果buff不够就继续喝药水用卷轴,不用心疼,后面应该也没有这么需要基础buff的卷轴/药水的地方了。
失陷教堂下面的石像鬼初始仇恨又都在主角身上,主角法师护甲+护盾术+镜影术拉满,还可以补渐隐术和移位术
边上山边捡队友,最终队伍配置是老四位+山茶岱兰(为了岱兰的行动自如和山茶的邪眼+巧手)
在教堂门口要给席拉用防死结界卷轴,防敌人的重伤术。看到高弗瑞的时候buff差不多掉完了,正好这里有清除腐化的雕像,可以休息一下再前进
然后下楼一路直走遇到泽卡琉斯,把魔杖给他解锁巫妖道途,我为了降低boss战难度同意打扰死者了。捡捡东西拆拆陷阱再上buff去两侧房间。这里有鬼魂,需要给席拉再撕一张防死结界卷轴。
打完回到地表,继续往前推进,石像鬼小怪没什么好说的,打最终boss之前给席拉兰恩主角(和其他你认为比较重要的队友)上行动自如,应该也不难打。打完获得神话2
打完捡东西,其他地方先不去探了下次再去,回山脚,离开,回营地的时候注意灰莓村有没有察觉出来,没有的话需要读档。
神话2:
主角 巅峰元素 火
席拉 盔甲专攻 中甲 耐受
山茶 想优先选的几个都没开前置专长,先不选了,等9级再
兰恩 精通重击 斩矛
聂纽 精通充裕施法
岱兰 持久法术
小烬 偏好超魔 增效
鸟哥 神话冲锋
索希尔 奇迹领域 疯狂
回营地卖东西,虚假希望链枷、魔法报应盾牌都卖了,购入炽焰火蛇给主角戴,又补充了两张防死结界卷轴,还剩1300+金币。
和队友对话给任务收尾,到努拉帐篷选诡计大师选项策反她,当前经验65374,睡一觉出门,这次岱兰换索希尔(感觉好久没带山茶索希尔了,调整一下法术位的搭配,我提前给索希尔记了两个行动自如备用),回失陷教堂,从这个地方下山脚

第一轮buff持续时间内一路打到了洞穴口。对石像鬼酋长用行动自如防控制,对邪教徒用防死结界防杀生术和重伤术,对魅魔用防护阵营免疫支配(以及之前上的防死结界免疫能量流失),它们弱强韧所以还可以让主角用咆哮术控。
打完魅魔群之后刷出来的垂线魔孽是这一段最难打的,有盲斗,高等隐形术对它无效。资源都可以交,席拉和山茶的屹立不倒我用在这里了TT
再往前是冒戈拉,会窃亡凝视,听到bgm变了先给前排上防死结界再往前,ac比较高但没有盲斗,让聂纽给兰恩上个高等隐形术就能打了。
然后我加速术移位术用得差不多了,好在剩下的都是小怪,第二轮buff一上全杀了。捡东西,跟爱露视频通话完就可以离开地图了。

回营地,卖东西,飞斧和手斧都卖了,之前的灵巧之拳护符也卖了,大猎物手套先留着 之后给爱露。购入霜护和骗徒戒指,都给山茶戴。至此第二章打算买的东西都买了。剩下的钱补充复原术、防死结界和行动自如卷轴。休息一下。
当前经验72429/75000,算上后面主线的1280经验,距离升级还差一千多。需要打一下灰莓村。
灰莓村:正常上buff,虽然席拉应该不太用得上但是以防万一。
潜行过去,一开始只有负责召唤的队友和主角靠近一点(防止人太多,boss放瘟疫风暴),看到boss之后岱兰召唤骷髅,山茶用在泽卡琉斯地下室发现的咒法与召唤的二元性召唤天使,还可以用酒杯召唤灵使,让召唤物去前排顶着骗技能,骷髅没了就补。如果骷髅拉好了boss的仇恨,boss朝骷髅放瘟疫风暴/灰飞烟灭就放不出来,而且天使还有电击抗性,不怕风暴束
召唤物拉住仇恨之后主角一直朝boss放魔法飞弹,兰恩清其他没被拉住的鬼魂小怪(记得上防死结界)。用上极效和强效权杖,主角放了3发强效增效魔法飞弹+3发极效增效魔法飞弹+2发增效魔法飞弹(还可以用德莱文的帽子送的瞬发加快速度)先打死了boss,剩下的就很好办,不用担心队友聚集导致boss放aoe了,直接群殴。打完就9级
获得了这个卷轴给席拉用
回营地再休整一下,捡的巨剑也可以卖了,继续补充那三种卷轴。圣教军可以往前推进了,记得把左边的军队也打了拿到力场之锋给主角(现在主角双持匕首,紫色石刀和力场之锋,一点也不像术士呢www威压木棍给聂纽了
不想做dlc4鸟哥任务了,直奔眷泽城!
9级:
主角:超魔 法术顽强,灼热射线,改专精灼热射线,狂笑术,加速术,高等隐形术
席拉:圣武士,盾击。新法术记武勇灵光
山茶:盔甲专攻-轻甲。然后神话2选盔甲专攻-轻甲-强攻
兰恩:受诅巫师(为了免疫疲劳),精通终势斩、跛足、野兔魔宠、冻皮
聂纽:技能专攻-知识-世界(为进博学士做准备),冰封之牢,定身怪物(现在聂纽有很多五环法术位了,记两个冰封之牢备用,剩下的都可以记延时高等隐形术,相对地四环就可以少记几个高等隐形术,改记延时加速术、移位术。变巨术缩小术也可以延时到二环、各记一个就够了(等buff时间结束也差不多要休息了,如果到时候发现还需要也可以临时喝药水顶着),一环多余位置记魔法飞弹,再记一个油腻术备用。总之好好调整一下。之后打眷泽城还是记双份buff(圣教军处已经获得了+4巨力腰带,给兰恩的牛之蛮力也可以不记了)
岱兰:高等法术专攻-塑能,熊之坚韧,祈祷术,防死结界
小烬:超魔-强效,治疗中伤,移除目盲,次元门(随便选的)
索希尔:超魔-法术延时(调节法术位用,四环好法术多但记不下,这样想用的就可以放到五环了
鸟哥:炫目武技,粉碎防御
眷泽城+10级神话3
打眷泽城了!没选雷吉尔的方案因为我不会用雷吉尔,但路线思路是和雷吉尔建议的一样的:走最短路线到城墙上杀巨人。
眷泽城内有3个休息点,加上女王和军需官那边(根据主角小队推进的进度不同)还会有1-2个。目标就是4-5次休息内打过达然赞德(打过之后就可以无限次休息了)。我玩的这周目只休息了两次就打了达然赞德,休息点还是绰绰有余的。
打之前的第一段路线规划(争取第一次休息前打完的):
进地图上buff,打完门口不得不打的小怪之后左拐,过两三次运动/灵巧检定爬上屋顶直接到达兵营里面(这里左侧门口有会放腐烂幻象的敌人,我喜欢绕过不打,想打的话用席拉的武勇灵光克制)
清理兵营,再下楼出兵营到神殿门口。神殿门口的敌人群比较烦,可以考虑用一张腐烂幻象卷轴。
打完神殿门口的敌人之后先不进神殿,过旁边墙上的检定爬上城墙,进入城内侧,去左侧的神殿后门。进门前迎面又是几只恶魔,杀掉。
进神殿,杀掉几只魅魔/淫梦魔之后再往前,有个妄乱魔信徒比较难打,走后门就是为了从后面打它,距离近一点第一轮不用跑太远,尽量把屹立不倒等资源留到这里。
打完下神殿一楼,靠近神殿门口的地方有两个会放腐烂幻象的敌人比较烦,好在回合制下不靠近就不容易被发现,可以在不被他们发现的情况下杀掉野蛮人,到对面发现隐藏墙和休息点。那两个会放腐烂幻象的太恶心了我就不打了,反正后面也不差这点经验。
到这里打得慢的话应该差不多两轮buff用完该休息了。捡捡东西卖给军需官,到神殿里休息。
实际情况下我打得比较熟练,打完妄乱魔信徒时第一轮buff才掉光,所以我就又往前打了一段。最后是打到图中这个程度,上城墙把巨人和弓箭手全杀了,第二轮buff时间还剩两分钟但我实在是不想打了。捡捡一路上的东西,卖给军需官,然后去教堂那边休息一次。
 捡到嗅血斗篷给兰恩装备,神圣轻弩可以先留着(后面看要不要给爱露用),其他新捡到的装备我都卖了。目前金币33600+,经验88599/105000。
捡到嗅血斗篷给兰恩装备,神圣轻弩可以先留着(后面看要不要给爱露用),其他新捡到的装备我都卖了。目前金币33600+,经验88599/105000。
休息过后从城墙尽头过检定下来去酒馆(如果还没打城墙就先打城墙上的巨人,反正路线是不变的)。酒馆里面这个怪比较麻烦,弱反射,我sl了两次用冰牢控它
从这里进监狱,门口有个会隐身的,用闪光尘打出来
 监狱里面还有一个会隐身的,还是闪光尘。半魔界牛头人ab比较高,可以交一个辟邪斩,提前走得离他近一点他就不容易冲锋。
打完把赘行魔放出来,拿到他身上的钥匙。目前教堂酒馆监狱三把钥匙已经集齐了。
和爱露对话,唱歌,爱露入队(但先不带她
开隐藏墙后面的敌人有点麻烦,我又用了一张腐烂幻象
监狱里面还有一个会隐身的,还是闪光尘。半魔界牛头人ab比较高,可以交一个辟邪斩,提前走得离他近一点他就不容易冲锋。
打完把赘行魔放出来,拿到他身上的钥匙。目前教堂酒馆监狱三把钥匙已经集齐了。
和爱露对话,唱歌,爱露入队(但先不带她
开隐藏墙后面的敌人有点麻烦,我又用了一张腐烂幻象
第一轮buff持续期间从酒馆一路打完了监狱,从另一个门口出来。第二轮buff期间到p2位置察觉了隐藏门,附近还有疾风弯刀(给席拉),进去杀淫梦魔,开大门,还能拿到第三个低等延时超魔权杖。又随便清了清之前没打的小怪(捡简单的打,没清完)。捡捡东西卖卖东西,第二次休息后就要杀小boss、准备进要塞内部了


第二次休息结束。目前金币64006,经验97713/105000。图中圈出的区域是绕过没有打的小怪,除了左下角因为赶时间绕过了之外,都是因为有会放腐烂幻象的怪,我嫌恶心不想打(还有神殿和酒馆里也有,也没打)。到左下角清一下小怪捡到守墓人头盔(卖掉),就可以去打小boss了

门口的堕落圣教军用席拉顶着,搜猎仪血量低,主角用两三轮魔法飞弹就打死了。
达然赞德有真知术和识破隐形,高等隐形术无效,直接打他又ac太高打不中,好在他身上buff的dc只有14。索希尔先给主角祝福,主角用解除魔法扒他buff,扒掉之后再让高等隐形术兰恩打他,一两轮就死了。注意用共用防护邪恶防止被支配


打完对话,就可以进要塞内部了。第一轮buff差不多够打到这里。其中会有一个有吸血鬼的房间,进房间前上共用防护邪恶防止支配,打完到棺材处杀死吸血鬼。后面用行动自如和防死结界应对食魂魔

再往前就是乔兰·卫恒了,措手不及ac也很高,主角可以出手(法系主角前期打小怪一般都不出手的,毕竟法术位有限),打完稍微往前走走再杀一个牛头人,就可以拐回头把前面错过的小怪打一打了。打完捡捡东西,再往前到如图房间察觉隐藏门和陷阱,房间内挂着的是假英勇之锋,过去拿会被埋伏,我就不过去了。出去卖卖东西休息一下,再回来打灾劫巨口(打完升10级

到献祭房间门口,上满buff,只有席拉进门,触发战斗之后先不打,等灾劫巨口被召唤出来,索希尔/山茶放召唤物顶着,主角放解除魔法解除它的真知术(不过它察觉也很高,还是有可能发现兰恩),山茶用邪眼降它ac,索希尔不断给兰恩善良之触/点滴幸运/疯狂愿景,高等隐形术兰恩砍,主角也放放法术打一打。打完升10级,获得斑斓炫目戒指,给聂纽了
10级
主角:超魔-强效,冰封之牢
席拉:无
山茶:等拿到神话3再升级
兰恩:野性诱变剂
聂纽:动物异变,心灵迷雾
索希尔:无
然后又往前走杀了两个牛头人,再往前是有很多波食尸鬼的地方,我又休息了一下。记得上防死结界和行动自如,初始仇恨在主角身上所以主角没必要过去,近战过去打就好了。打完继续往前,看到解谜环节,直接放aoe能打出隐身的敌人,打完解谜,拿到英勇之锋,拿到之后马上出现一波小怪,打完捡完东西上楼,进灵使道途了!!
神话3
主角:偏好超魔-强效
席拉:常备不殆
山茶:第二精魂-流风。然后升十级:空气屏障
兰恩:常备不殆
聂纽:偏好超魔-延时(下次休息之前就要大改法术位了
索希尔:偏好超魔-延时
到这里第一轮buff也掉光了,进要塞内部用第二轮buff打。重新进要塞之后没几波小怪了,人多的地方就扔腐烂幻象卷轴,主角扔扔火球术,不用省资源。
没注意什么时候捡到了虫壳甲,捡到就可以给席拉换上了,虫壳甲虽然写着是重甲但是也吃中甲耐受的加值

到冥娜蛊门口休息一下,记得给点了偏好超魔延时的队友的法术位好好改一改。最终boss战集火斯陶顿就好,有什么用什么。进第三章了!!
第三章
第三章打算买的东西
军需官:
次元袋
织秘者:
秩序长袍(兰恩
决斗手套(兰恩
使节手套(沟通
珠宝商:
明晰镜饰(法系
纯净视域眼镜(法系
心灵大师之眼(惑控法
牧师:
纵火狂戒指(法系
出双入对(前排
酒馆:
邪眼护目镜(兰/其他察觉人
冬阳村:
贵重款待(岱
灵使花园:
精准手套(爱露
凶猛契约护目镜(爱露
鸟哥任务地图商人:
玫瑰刺弹药箭筒(爱露
炽焰弹药箭筒(爱露
灼热护腕(主角
集群克星搭扣(根据实际需要
dlc3商人的菜谱和做菜原料
打dlc3拿:
永寒(爱露
不宣之实长袍(法
无可辩驳眼镜(法
残缺诡术师(席拉
精灵之靴(灵巧
第三章初期准备+10级神话3
找酒馆老板和伊拉贝思能分别领到一万五和五万金币,谢谢打赏啊!
雇了葛雷博,之后直到完成猎龙任务之前都最好备着共用防护火焰,以防万一
买了纵火狂戒指和纯净视域眼镜提升一下主角的法穿,秩序长袍和决斗手套给兰恩,使节手套给岱兰(不带岱兰的时候可以自己戴),还找军需官买了次元袋
城里捡到的书记得看,又有两本可以给主角提供加值的
打眷泽城没带的其他队友的升级加点:
小烬:强效救难,疲乏波,偏好超魔(强效)
岱兰:真知术,高等持久法术
鸟哥:血怒者-混合血怒者,无限狂暴
葛雷博:运动,察觉,使用魔法装置,机会主义者
爱露:沟通和神秘不点了(主角和聂纽负责),换成使用魔法装置和宗教(或许可以做重压之刃卷轴给近战用?但要学一个抄录卷轴,之后再看吧),精通先攻;精通重击-重弩(用过轻弩,没用过重弩,这次试试看!),宿敌-不死生物、魔法型恶魔,变化自如、快速射击、领袖感召
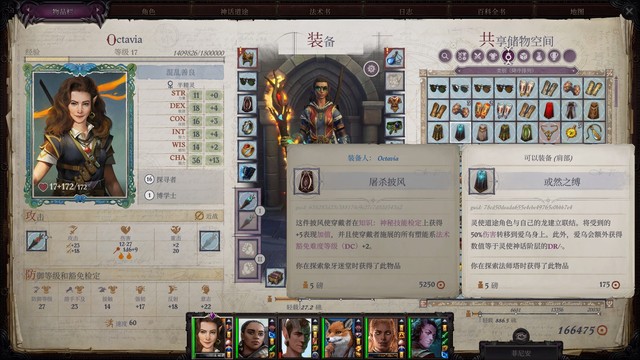
山茶身上的好装备可以脱下来给爱露了,接下来带爱露负责巧手/灵巧等检定,下次出门除了灵使地图 差不多就直奔绿门堡(爱露法术位我主要就用一环的飓风之弓、隼之型,二环识破命门、猫之轻灵,三环视如寇仇)
下次出门预计队伍是老四位+爱露+索希尔,岱兰还是等他再学几个常用法术再带
灵使道途可以先出发去灵使后花园看看,看完回城,正好议会组建好了,开会
捡沃尔吉夫(+升级)+dlc4第二章任务+绿门堡+熔火之痕
从眷泽城出发一直往南,触发事件,看到敌人在谈论深渊的新月
击败后离开地图,回到失陷教堂再向西边走,第一个路口不管,第二个分岔路走向斜下方,再次触发事件,就捡到狗了
沃尔吉夫加点
9级:突刺,接触魔法、共用识破隐形(其实三环常用的都已经让他学过了,这里随便选的)
10级:共用防护能量、高等隐形术
神话2+3:双武器战斗、大法师护甲
捡完沃尔吉夫回眷泽城,爱露任务(去绿门堡)正好触发了,之后再去。
回城,到军营附近找西尔金德接隐藏任务,卖垃圾,购入了心灵大师之眼给聂纽,又补充了两张复原术,办完事之后换队友(席拉 鸟哥 聂纽 索希尔 爱露)去灵使后花园休息一下(获得如图buff),然后去做鸟哥任务

聂纽的低等延时超魔权杖可以卸下来换给爱露(以及沃尔吉夫等人)用了,鸟哥第二章任务这个等级再打已经相当简单感觉没什么好说的,就是注意上防死结界、菲尼安变武器给爱露用这样能打出伤害,其他怪的应对方式之前都提过了

这次回城触发了岱兰恋爱剧情、朝暮剧情、索希尔个人任务。卖垃圾+做一下索希尔任务+和乌布里格对话,再重新出门,去绿门堡。记得把之前从兰恩身上扒下来的装备还回去
去绿门堡路上会触发红龙事件,记得提前准备好共用防护火焰,顶住两轮它就会走了
到绿门堡满buff,需要共用防酸。阿罗登之怒给席拉,风宗头盔给爱露(或者其他需要先攻的),脱缰之靴给前排(就可以少记一个人的行动自如buff),其他装备不用的话可以卖掉
打完去熔火之痕,不难打,过威吓拿到纸,之后可以给说书人。秘法根除手套可以给主角打射线用。传送回城吧
亵渎神坛+11级+善猎神殿+灰白岩洞+沃尔吉夫任务
交交任务,卖卖垃圾,购入明晰镜饰给聂纽、邪眼护目镜给爱露,再次出门。距离升级还差一点点经验,这次去亵渎神坛,打一点就升11级了
11级
主角:超魔-甄选,强酸箭、重挫冲击、灭顶悲恸、驱逐术(之后阿瑞露实验室可能就有用)
席拉:双武器战斗,力竭
聂纽:博学士,超魔-甄选,法师专长-超魔-顽强,酷热之风、高等英雄气概
爱露:(试试看这种玩法!)歌者-宫廷文豪,余音绕梁,超魔-延时(因为宫廷文豪唱歌给全队加智力和魅力,相当于加强主角和聂纽(而且记得爱露在后期命中也不是特别高,打boss比较难命中,就觉得不如让她在攻坚战多负责辅助好了
索希尔:解法专攻
兰恩:武器专攻+高等武器专攻-斩矛
山茶:精通重击-细剑
小狗:熟练偷袭者,短剑,次元门、石肤
岱兰:超魔-甄选(预备之后放甄选颂圣之语),动物之友,共用防护阵营、共用抵抗能量、维生气泡
小烬:技能专攻-神秘,熔融球,移除诅咒,弱能术,洞窟獠牙
鸟哥:化形师多重攻击
葛雷博:突变斗士,包抄,突刺
升完级再打这个地图的boss就没那么难了,震电斩可以给沃尔吉夫玩玩
回城触发了黑水任务和岱兰送礼,卖卖垃圾去趟天堂之缘,把岱兰藏的礼物拿出来
圣教军处拿到的蜻蜓链甲我给索希尔了,反正他平时只辅助、不去前排战斗。换下来的生机半身甲卖掉了,去灵使地图买了精准手套给爱露(以后打小怪戴这个、打boss戴大猎物手套好了),休息一下。
然后去善猎神殿:笛拉梅尔的盔甲可以先给爱露用着,弓有阵营限制就算了
灰白岩洞有术士主角就很好打,扔几个甄选增效火球术就过了
沃尔吉夫任务,迪瓦尔身上敲诈来的稳定之指给主角,替换炽焰火蛇,炽焰火蛇给的法术超魔后就会留在法表里了,所以卸掉也没关系
沃尔吉夫任务还拿到了恶魔之影腰带,先给聂纽用着
圣教军那边,用破晓无缺做个凯旋正午给席拉用
然后回城,触发了灵使任务,可以休息一下去阿瑞露实验室了。钱正好够买凶猛契约护目镜,买一下
阿瑞露实验室
到阿瑞露实验室了,剧情后就是探索和战斗,因为后面可以拿到神话4所以我就先直奔神话4去了,一路上一直直走,不打两侧房间里的怪,等拿到神话4再打
神话4
主角 反应施术 卓越魔法(帮聂纽控人)
席拉 盔甲专攻-中甲-强攻
兰恩 猛力攻击
聂纽 反应施术
索希尔 奇迹领域(联盟)
爱露 精通重击(重弩)
山茶 精通重击-细剑
狗 常备不殆(悲伤地发现精通重击/精通先攻/轻甲专攻都没点……
烬 反应施术
鸟哥 武器专攻-爪抓
岱兰 法术专攻-塑能
说是回合制但其实现在已经会偶尔在非常有把握的时候开即时制加速战斗了(我开了战斗动画3倍速,即时制下打得很快
灵使新法术很好,成为常驻buff了
继续打,这个房间的遁影魔弱意志,聂纽用虹彩图/灭顶悲恸控了。旁边小房间拿到落魄重弩,给爱露换上。
 再往前房间的毒啮魔弱强韧,主角用甄选咆哮术,六臂蛇魔ab比较高,真顶不住就等休息完再来用屹立不倒顶
另一个房间的纳祭魔,打法1开局迅速控+杀其他小怪防止它们控制队友/扰乱战局,再和纳祭魔硬碰硬,它造成的眩晕用席拉的圣疗解决。打法2开局迅速集火在纳祭魔上完buff之前秒了它(需要运气,我兰恩不到两轮出了三次重击才秒掉)。都用上了炉台守卫。旁边房间的袍泽头盔给席拉戴上
再往前房间的毒啮魔弱强韧,主角用甄选咆哮术,六臂蛇魔ab比较高,真顶不住就等休息完再来用屹立不倒顶
另一个房间的纳祭魔,打法1开局迅速控+杀其他小怪防止它们控制队友/扰乱战局,再和纳祭魔硬碰硬,它造成的眩晕用席拉的圣疗解决。打法2开局迅速集火在纳祭魔上完buff之前秒了它(需要运气,我兰恩不到两轮出了三次重击才秒掉)。都用上了炉台守卫。旁边房间的袍泽头盔给席拉戴上
阿瑞露实验室其他房间应该不难,有晶簇的房间我嫌烦就不打了,正常打的话可以先贴着走廊另一侧走不触发战斗,拿完神话4(的二环法术提升法穿)再回来对它使用驱逐术
拿到的有用的装备:追击寒铁细剑(山茶);袍泽头盔(席拉),落魄重弩(爱露),+4智力头带(聂纽),古代令使斗篷(索希尔/岱),反射线小圆盾大概也能给山茶用用,古代斗篷碎片大概要第四/第五章才能修复了。
圣教军处用沦亡骑士(后面忘了)做了马兰德腰带给主角(有污邪附伤的那个
回城把不要的装备卖掉发现居然有了8万,购入出双入对,目前城里打算买的装备都买过了
兰恩任务+冬阳村+12级
兰恩任务,我选择杀了雯朵格,获得无情射杀戒指,爱露ab不够的话可以给爱露。下次,做鸟哥任务还是去冬阳村呢
回城,灵使选支持骑士团做雕塑之后获得了新休息加值
休息完去了冬阳村。最难打的(旁边能看到一群恶魔围着打的)树人先放着,等之后做发疯女精灵任务第二次去的时候再顺便打。
除了常规buff之外,在地图右下角需要防酸,另一个角带动物伙伴的萨阔力游侠处需要防箭
洞穴里的毒啮魔,我让聂纽用定身怪物控了(法穿21+1d20 vs 法抗29;法术难度34 vs 意志豁免25),席拉和兰恩免疫他的死云,控住之后就好打很多
再往前,莫维格ab比较高,可以用屹立不倒顶一下。ac和反射都不高,顶住就没问题(倒是也很符合剧情……)
恶意之牙一会儿别在冬阳村卖了,回去找塞珥有对话
路上遇到的立石上面的世界检定一定要过,全过之后有奖励
村子马赫沃克房间需要防箭和防冰,龙用强效增效火球术打,马赫沃克用定身怪物控(提前上共用防冰、黑暗罩纱),打完做完任务(同意保持现状+同意她带走马赫沃克)马上12级,杀杀外面的小怪升个级,然后去洞穴里休息,休息完正好清除腐化
保持现状后村里出现新的淫梦魔商人,找他购入贵重款待给岱兰、伟岸雄姿卷轴给聂纽学
地图清了这么多之后12级了,休息。有个石墓上的尸体身上有装备,拿了要和幽灵开战7次,我下次来的时候再拿。
休息前记得先升级、整理法术位

12级
主角 酷热之风
席拉 无
兰恩 一人成军 武器训练-长柄
聂纽 博学士 焦油池 共用石肤(想着不知道选什么了,学一下这个抄成卷轴用吧,结果学完发现索希尔也会
索希尔 无
爱露 敏捷 (学会狩猎目标了好耶!
茶 战斗大师-细剑
狗 机会主义者 恐惧术 高等动物之型
烬 康复 高等解除魔法(真的基本都是乱选的、因为这周目火法有主角了
鸟 巫师 受诅巫师 野兔 冻皮 跛足(免疫疲劳,下次做鸟哥任务就舒服多了
岱 共用真知术
葛 突变斗士 力量 盔甲专攻-中甲(神话等级:屹立不倒、盔甲专攻-中甲-耐受、常备不殆、盔甲专攻-中甲-强攻。换上之前席拉换下来的中甲
主角12级能放6环法术之后记得再换上一下炽焰火蛇戒指,给地狱烈焰射线超魔留在法表里之后再换回来
继续探索,在萨阔力流亡暴徒那边再用一次黑暗罩纱。弱意志,聂纽可以扔一两个群体控制。
最后打完整个冬阳村的地图是这样,难打的树人以后再来打
 左上角洞穴里的索亚纳可以喂山茶(但我没喂
离开地图,回眷泽城。卖垃圾,对话完成任务,找塞珥。
军需官给指挥官礼物了
找兰恩和苏尔对话,触发兰恩做酋长事件
现在已经存下13万了,下次做猎龙任务和鸟哥任务,正好雇一下葛雷博,再在鸟哥地图商人那里花花钱
左上角洞穴里的索亚纳可以喂山茶(但我没喂
离开地图,回眷泽城。卖垃圾,对话完成任务,找塞珥。
军需官给指挥官礼物了
找兰恩和苏尔对话,触发兰恩做酋长事件
现在已经存下13万了,下次做猎龙任务和鸟哥任务,正好雇一下葛雷博,再在鸟哥地图商人那里花花钱
猎龙+银龙巢穴
猎龙配队思路:主角 山茶 葛雷博 聂纽 爱露 索希尔,用邪眼+狩猎目标和游侠羁绊+炉台守卫+索希尔的其他辅助能力使劲缩小葛雷博的ab和龙的ac之间的差距
进去先埋伏,等到龙出现再上buff
然后战前buff+炉台守卫+狩猎目标+邪眼(ac)+研究目标,葛雷博直接一轮秒了


追龙,路上的检定通过sl全过,这样才有时间上buff
复刻上一次的打法(主角还可以放放射线),把龙打跑之后马上去追,不然好东西会被烧掉,然后捡完东西就可以回城了(楼下的怪的懒得打)
回城后卖垃圾、和说书人对话,给他看龙爪
调整装备,出双入对给席拉和兰恩戴,下次去银龙巢穴,还是老配队(主角席拉兰恩聂纽爱露索希尔)
此时触发了兰恩恋爱剧情,和兰恩打拳自动卸下所有装备,主角转混乱善良了戴不了德莱文的帽子了……含泪交给聂纽……
忘了什么时候拿到的召唤戒指(圣教军掉落的还是说书人修复的?),反正先给索希尔戴了(谁手上有空位就谁戴

圣教军处给叛徒家园升级,造传送门
去银龙巢穴的路上有荒野遭遇(共用防火)和损毁的长屋(防死结界)(记得补充防死结界卷轴),顺便一起打了
银龙巢穴没什么好说的,解锁金龙道途。打完顺便去神秘之心(拿到黑暗面具和精灵笔记)和下面的污蚀古冢(过检定,最后选拿值钱的东西,获得剑师之赐给兰恩)
圣教军处幽径之石做戒指
传送回城,去灵使花园,做下一段任务+卖垃圾+休息
dlc4第三章任务
配队换成主角席拉鸟哥聂纽爱露索希尔
目前有两个克集群吊坠,鸟哥一个爱露一个,地图右下角洞穴里的大虫子弱意志,控一下再用射线打就好,鸟哥用死神天降打,小队站位分散一点免得被集群全控了,在它逃走之前打掉,多拿点经验
保护车队的任务,进地图之后再上buff,用上黑暗罩纱。鸟哥用死神天降优先打对面远程,实在恶心(因为敌人初始仇恨都在主角身上)就把炉台守卫也放了
进森林之前的所有战斗都打完了,正好buff用得差不多了,休息一下(多记几个防死结界)。猫头鹰兜帽和猪突猛进护腕都给鸟哥,后者等做完鸟哥任务还可以给兰恩
第一次休息前打了这些,洞穴没进去,调整法术位休息一下再打
一个洞穴里的冷血狂怒xxxx,弱反射(20),用冰封之牢控,还可以用高等解除魔法扒buff。常态ac55,控住之后就好打多了。他也是虚体,菲尼安变重弩给爱露用就好了(+视如寇仇),他下一轮挣脱控制了不过也没关系,已经只剩血皮了
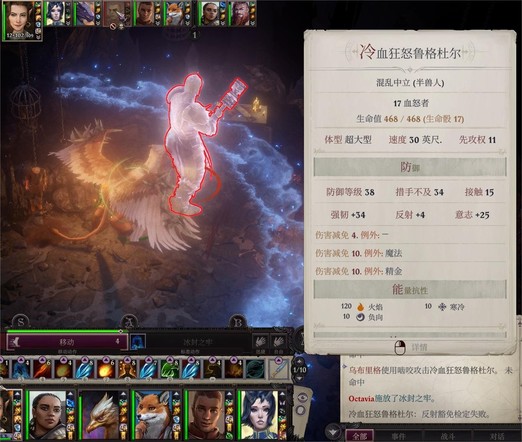
另一个洞穴里的书虫xxxx,进去之前先上共用防护能量(但我这次第一轮就控住了第二轮就杀了,没看他会先用什么元素的攻击),同样弱反射,控住,鸟哥优先死神天降过去杀掉。其他小怪不难对付。
两个洞穴打完获得两把钥匙,打开森林入口处的门,里面的怪不知道能不能打过,休息一下再试试。(还有休息一下到晚上,把晚上才能做的祭坛处精魂任务也做一下)
还有地图中间往左的哀痛呼唤者和一群塑能师(上周目居然都没发现这个地方……),哀痛xxx会高等隐形术,过去察觉出来之后还是鸟哥死神天降解决,只要抢到先攻就不难打
森林入口处的门内的法师技能离谱但血和ac都没有很高,所以先杀法师,爱露上高等隐形术潜行射一箭开突袭轮,鸟哥擒抱(但我没控住),主角射线,爱露狩猎目标+视如寇仇,突袭轮后第二轮就杀掉了(第一轮献祭了爱乌

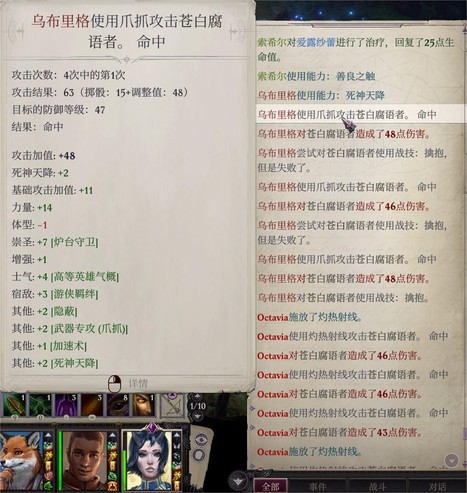
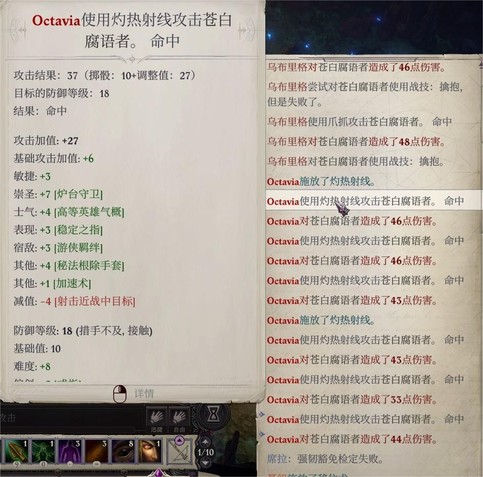

没了法师就好打很多,另一只初始ac65但ab没有很高,席拉还有屹立不倒,可以顶一段时间,索希尔用纯净视域眼镜送的一次高等解除魔法大成功解除它的buff,解除之后就好打一些了,还给一万经验和高等瞬发超魔权杖,早打早享受

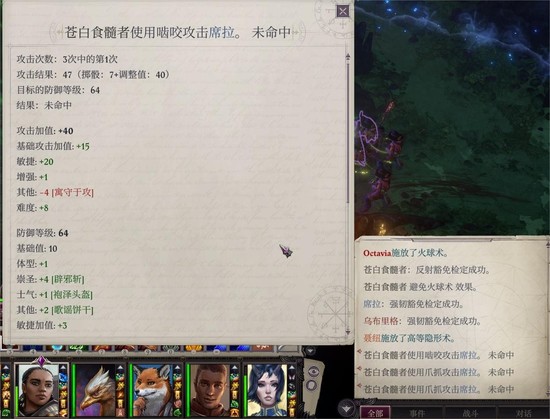

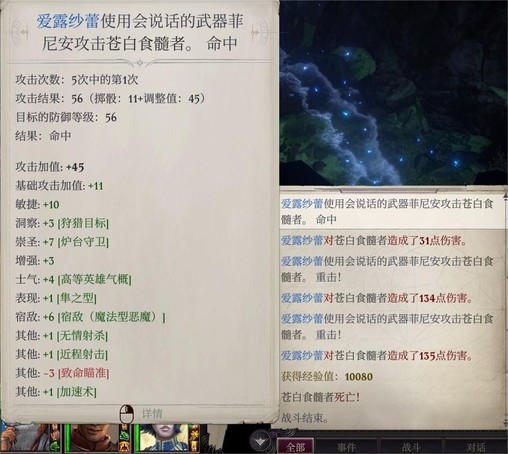
鸟哥任务地图全清之后是这个经验,快升级了,回去做做队友任务(雷吉尔的应该触发了),等13级就去象牙迷堂

雷吉尔任务+绯红之尘+旧萨阔力矿坑+13级、14级
配队是主角兰恩雷吉尔爱露索希尔聂纽,路上顺便去dlc3商人那里买东西,直接买了橡子馅饼(+2dc)、恶魔杀手汤(+3攻击和伤害检定)、炽热玉米卷饼(全属性+4)的菜谱和对应的食材99份,这下能一直吃到结局了
雷吉尔ac如图,临时替席拉t一下。进战斗之后(不用辟乱斩和神爪骑士团什么的),袍泽头盔给的ac少掉2左右,狂暴-2ac,防御式攻击+4,最后也差不多是这样……
 雷吉尔任务地图满buff就很好打,捡到速杀匕首给小狗贼用。
雷吉尔任务地图满buff就很好打,捡到速杀匕首给小狗贼用。
绯红之尘没什么好说的,不难打,给的经验还多
地图里的剥皮斗篷可以给爱露,反正我目前也没拿到更好的(

旧萨阔力矿坑这边的两个自然检定给好多经验,整个地图调查完就升13级了。回城一下休整一下续一下灵使特殊buff,下次直接去象牙迷堂

13级
主角 元素专攻-火 技能专攻-神秘 高等解除魔法 专精-地狱烈焰射线 魅影杀手 剧痛射线 高等英雄气概
席拉 盾牌大师(学会正义烙印了好耶!
兰恩 突刺 抓准时机
聂纽 博学士 精通先攻 游荡者-野兔魔宠 群体定身他人 高等解除魔法
索希尔 高等解法专攻
爱露 武器专攻-重弩
茶 突刺
狗 轻甲专攻 回声定位 共用石肤
烬不在,之后再升级
鸟 野蛮人-先觉斗士(感知加值加在先攻检定上) 延时拟态
岱 法术专精-剑刃障壁 共用防护能量 荣光爆发 剑刃障壁
升完级记得给队友填充法术位
圣教军处做好了马兰德的耻辱腰带,给主角(火伤+2d6污邪附伤
席拉拿了盾牌大师(彻底取消盾击的双武器战斗减值)就可以开盾击了
圣教军处还获得了这个戒指
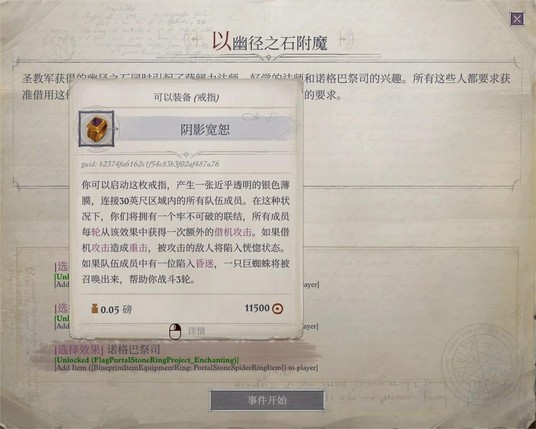
回城,触发了小烬任务,找西尔金德交任务,帮兰恩和妈咪贴贴,卖垃圾,回灵使花园睡大觉。下次去象牙迷堂!
灵使新buff

- 纯净视域眼睛送的一次高等解除魔法大成功,使用后就会留在人物身上成为永久buff直到被使用,而物品的这个能力每隔一天刷新一次使用次数,所以理论上可以在需要解除魔法的战斗之前给所有会解除魔法的队友都弄上这个buff(反正我先给主角和索希尔都整上了
象牙迷堂+龙族墓地+席拉任务
进门战斗挺简单的,防火就好。过剧情同意合作。
在中间圆形场地拿到战斗法师木棍、旁边解谜拿到屠杀披风,给主角
到这个房间记得做好打集群的准备+防死结界+防护火焰,优先打被转变的食魂魔
打完踩机关+察觉按钮开门,隐藏房间里有灭惧者戒指(我一般卖

然后我直奔boss房了。打贤希尔之前休息了一下,叠了餐食加值。贤希尔免疫高等解除魔法和正义烙印,但不免疫困惑(被索希尔的疯狂灵光搞得自己打了自己召唤出来的小弟……
然后进二阶段了,变虫群,提前给席拉兰恩爱露爱乌都换了克集群吊坠,索希尔抬血,主角一轮扔两个火球术(瞬发一个),很简单了。没有吊坠也没事,有人能扔(有巅峰元素-火+增效+强效+极效+瞬发+马兰德腰带附伤等等的)火球术就行,减伤就用共用防箭。
第三阶段贤希尔又变身,这次更是好打,兰恩砍、主角射线,一轮就死了
然后和贤希尔对话,告诉他虫群会被ntr,激怒他起来再打一次(有更多经验)
这次他召唤的小弟和虫群一起出现,场面挺乱的……反正我就还是兰恩砍贤希尔,主角扔火球术,就过了……(过了……(可怜的爱露被恶意变形术变成狗了,对她使用大成功的高等解除魔法吧
在这里捡到的书记得看,有加值。
打完boss就放心了,过完剧情继续推其他地方。休息之前打了这些,应该基本上只剩下面的永恒守卫了

有宝箱怪的房间旁边的隐藏门里,有机关会给永恒守卫回血,我的打法是席拉进去触发战斗把永恒守卫拉出来,其他人在宝箱房门外等着。现在席拉索希尔爱露都在的时候,ab已经相当容易叠起来了
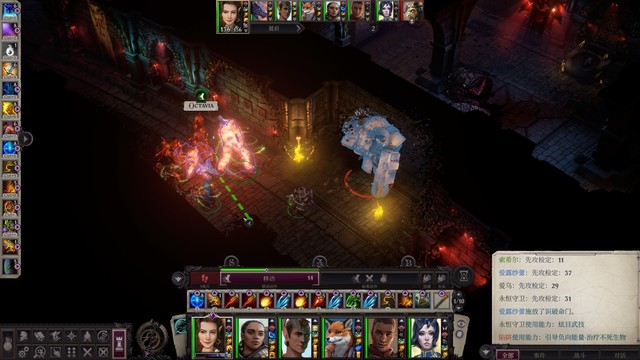 拿到恶魔愤恨给兰恩戴。打完就可以走了,这次回去路上必定触发卓尔精灵的任务事件,记得提前留好buff/休息一下
当前经验418458/445000,又快能升14级了
拿到恶魔愤恨给兰恩戴。打完就可以走了,这次回去路上必定触发卓尔精灵的任务事件,记得提前留好buff/休息一下
当前经验418458/445000,又快能升14级了
传送回城,卓尔精灵任务事件结束后看手哥剧情。城内休息一下,去做赞妮德拉任务,很好打。打完去龙族墓地和席拉任务,感觉也没什么好说的……打完就14级了。
14级
主角 狮子吼
席拉 目盲
兰恩 野性之翼
聂纽 博学士 迷醉波 寒冰之躯
索希尔 无
狗 巨灵化身 动物异变
鸟 突变斗士 精通先攻
岱 颂圣之语
其他人也不怎么带,懒得好好点了
黑水+圣地
配队是主角席拉兰恩聂纽索希尔爱露,可以提前准备一把精金武器以防万一(比如精金大砍刀裂魂者,眷泽城斯陶顿掉的)。门口捡到召雷魔杖,可以给合适的队友提前装备上,后面补刀用。进大门之前上常规buff+共用防护电击
进门触发动画开始战斗,敌人法师会用音爆哀鸣,席拉的武勇灵光可以克制
敌人需要受到电击伤害才会彻底死亡,可以用门口捡到的召雷魔杖,也可以用聂纽的放电戏法(或者其他能造成电击伤害的队友,比如学了召雷的法系人,甚至是可以给细剑电附魔的山茶
然后发现前面的门打不开,需要密码。右拐,在图中这个房间触发战斗。
 再往前,看到增强火蜥蜴,杀,捡东西,拿到炸弹(但不想捡东西的话应该也可以不杀……?反正这边有用的只有用来开门的炸弹,而门可以用密码开),回到正门口,这次向左走,两侧的门先不用开,一路往前走
再往前,看到增强火蜥蜴,杀,捡东西,拿到炸弹(但不想捡东西的话应该也可以不杀……?反正这边有用的只有用来开门的炸弹,而门可以用密码开),回到正门口,这次向左走,两侧的门先不用开,一路往前走
在图示房间清除敌人之后和仪器互动,获得权限,还捡到了火焰开锁器
(发现黑水还有敌人的阵营是守序善良,唉)
刚才捡到的火焰开锁器可以炸开来的路上打不开的门中的一扇(门内有一份开锁器燃料和我打算卖的武器),获得权限后也打开了一个房间(门内有密码最后一位的提示:
 目前地图右下角彻底探索后是这个样子:
目前地图右下角彻底探索后是这个样子:
 刚才有火蜥蜴的房间门外的敌人忘记对话了,对话获得密码前两位:
刚才有火蜥蜴的房间门外的敌人忘记对话了,对话获得密码前两位:
 现在大门可以打开了。打开之后来到图示位置,前面圆环型平台上的战斗是第一处有难度的战斗。
现在大门可以打开了。打开之后来到图示位置,前面圆环型平台上的战斗是第一处有难度的战斗。

到圆环平台上,上防死结界防魅魔的能量流失、共用防护邪恶防支配(不过我忘上了,魅魔也没使用支配)。
平台上敌人ac比较高,需要爱露用游侠羁绊(+大猎物手套+狩猎目标)。擒奴魔弱意志(聂纽控),魅魔弱强韧(主角用咆哮术/狮子吼控),控住就很好打。



 目前聂纽的法穿有了灵使的+4法穿buff之后就也够打小精英怪了,惑控和幻术系法术的dc也够用。反正有德莱文的帽子,一发没控住还可以瞬发补一下。主角的咆哮术超魔后dc更高,还有卓越魔法,很好控。
圆环平台上的敌人还有电击抗性,我这里打倒之后用召雷魔杖/电戏法补刀有可能过不去电抗。但精金也可以破再生,所以说可以准备精金武器。看别人说等敌人倒地之后用致命一击也可以,我没试过。
(发现共用防护箭矢卷轴用完了,记得之后做一点备用)
目前聂纽的法穿有了灵使的+4法穿buff之后就也够打小精英怪了,惑控和幻术系法术的dc也够用。反正有德莱文的帽子,一发没控住还可以瞬发补一下。主角的咆哮术超魔后dc更高,还有卓越魔法,很好控。
圆环平台上的敌人还有电击抗性,我这里打倒之后用召雷魔杖/电戏法补刀有可能过不去电抗。但精金也可以破再生,所以说可以准备精金武器。看别人说等敌人倒地之后用致命一击也可以,我没试过。
(发现共用防护箭矢卷轴用完了,记得之后做一点备用)
打完对面三扇门,只有中间一扇能用火焰开锁器炸开,炸开后继续往前,左边房间里又是魅魔和擒奴魔,同样的打法。
然后就一路探索地图左下角这一片区域,这个房间是小boss,我在这里把炉台守卫交了
 小boss这边敌人ac没有刚才那么高,需要和装置互动解除屏障才能打到高台上的敌人。弓箭手比较烦,黑暗罩纱也可以用一下,以防后排被射中
小boss这边敌人ac没有刚才那么高,需要和装置互动解除屏障才能打到高台上的敌人。弓箭手比较烦,黑暗罩纱也可以用一下,以防后排被射中
打完获得新权限,左下角目前探索完是这个样子,圆环平台处的最后一扇大门可以打开了
 我玩到这里的时候加速术移位术高等隐形术buff用完了,休息一下
我玩到这里的时候加速术移位术高等隐形术buff用完了,休息一下
探索地图左上部分,在这个房间获得百面的头环组件

在这个房间和npc对话,并获得火焰开锁器燃料

回到地图右下部分,打开之前打不开的门,里面有百面头环、心胜于体戒指和风暴领主的决意

回到左上有npc的房间,使用仪器,这样就可以打开有紫色保护的门了
能去的小房间全部探索后地图是这个样子,有个地方需要和装置互动,顺序是手、风(或 风、手,不记得了,反正没有火),互动后在打开的门里获得一把武器。左上就是boss房

打boss之前记得上共用抗电和防电,开局队友分头把周围的四个装置关掉,就可以打到boss了,百面ac很低,豁免也不高,很好打,集火就好
(主角上高等隐形术的话,有可能结束对话时并不马上触发战斗,可以趁这时赶紧去关装置)
武器库在这里,拿到巨剑,就可以走了

从黑水出来顺便把旁边的圣地打了(贴吧有解谜攻略),灵使可以让旁边的树木活过来帮忙t第一轮,恶魔弱强韧,我主角第一轮用狮子吼+反应施术的咆哮术控住了,其他队友迅速跑过来顶住就好,有队友在就很好打,有什么buff全都往上扔就行,反正打完就回眷泽城



dlc3+索希尔任务+15级
目前第三章除了冬阳村发疯女精灵任务和索希尔任务之外都触发了,收拾收拾去dlc3坐牢
dlc3如果在主线玩,岛的流程就是固定的,第一个岛很简单没什么需要注意的地方,重要战利品:永寒(给爱露,虽然只是+1重弩但它能让你多射一箭而且还带控制
岛2同样很简单,14级去打就是碾压,重要战利品如图。打完两个岛之后法术用得差不多了,休息一下


岛3:
岛4同样不难,敌方法师的控制法术烦但豁免低,先手控住就好。重要战利品如图。重载了,出去卖一下垃圾再回来继续打,顺便处理一下圣教军事务
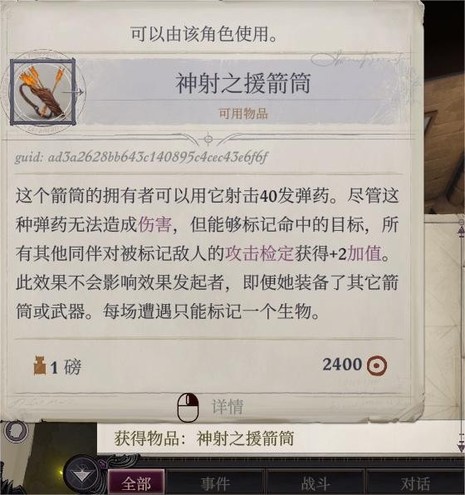

在灵使花园休息完,回城正好触发了索希尔任务。也很好打,弱意志,控一下就行了。要注意的是打完之后有个通过运动检定上去的土坡,背包里有一点好东西,捡东西触发幽灵战斗,记得提前上防死结界
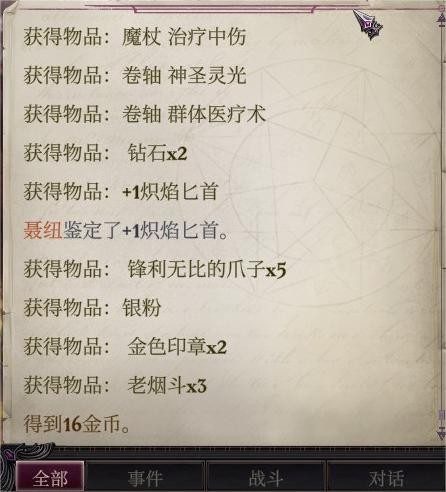

岛5需要抗火+防火,p1的怪会放地形法术比较烦(忘了是什么法术了,这周目没让她放出来就杀了),弱反射,用冰封之牢控。战利品如图,卫士盾牌或许可以给点了盾击的葛雷博

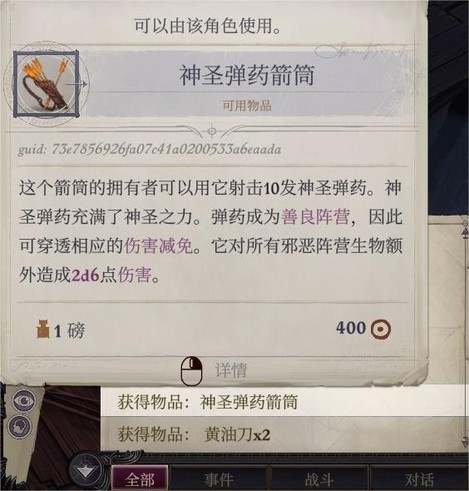

岛6需要抗寒+防寒,依旧是用冰封之牢控对面祭司,战利品如图



岛7妄乱魔信徒比较麻烦,可以优先击杀。主要战利品:(我打算给山茶)。打完休息一下
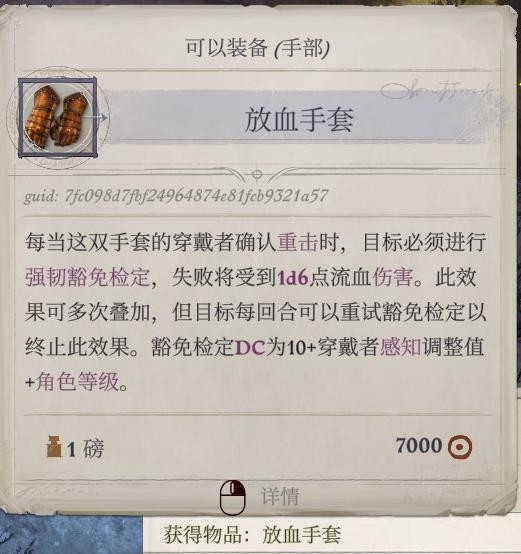
岛8感觉没什么难的,战利品如图

岛9开始敌人的ac稍微高起来了(虽然兰恩ab还是很高的所以不怕),弓箭手的ab也比较高,可以让席拉针对性用一下镜影术魔杖和辟邪斩,防止过早被弓箭手打出屹立不倒



还是岛9,妄乱魔信徒免疫麻痹但是不免疫震慑,用咆哮术控。战利品如图。因为最后敌人的阳炎爆目盲了,还好提前准备了移除目盲卷轴


打完岛9,聂纽的加速术移位术高等隐形术buff还剩一份,所以进岛10稍微打一打把buff用完再出来休息。岛10的特殊效果有点烦,好在主角是法师,算是利大于弊吧
 ……结果就这样把岛10打完了,不够的辅助用药水和索希尔的领域能力来凑,最后交了炉台守卫(第三章以来大家的法术位用得最干净的一次),地图末尾刚好有雕像恢复状态。战利品如图,岛9的眼镜和这里的长袍适合智力系法师,给聂纽了
……结果就这样把岛10打完了,不够的辅助用药水和索希尔的领域能力来凑,最后交了炉台守卫(第三章以来大家的法术位用得最干净的一次),地图末尾刚好有雕像恢复状态。战利品如图,岛9的眼镜和这里的长袍适合智力系法师,给聂纽了

岛11有集群,提前换上克集群饰品、准备复原术卷轴。最后boss的ac比较高还有隐形术移位术,先用高等解除魔法扒它buff再打,我这边刚好还用卓越魔法狮子吼控住了。


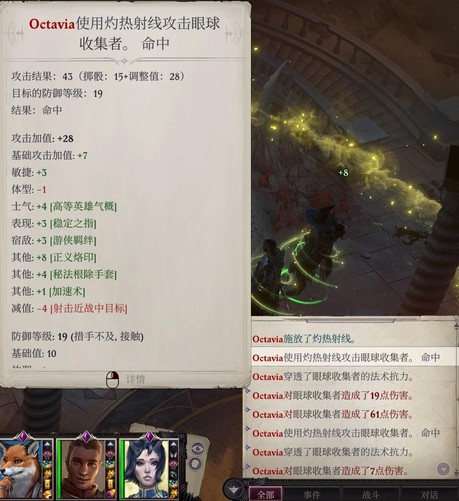 战利品如图,还有一个猛击之盾,但感觉不如席拉现在用着的凯旋正午
战利品如图,还有一个猛击之盾,但感觉不如席拉现在用着的凯旋正午
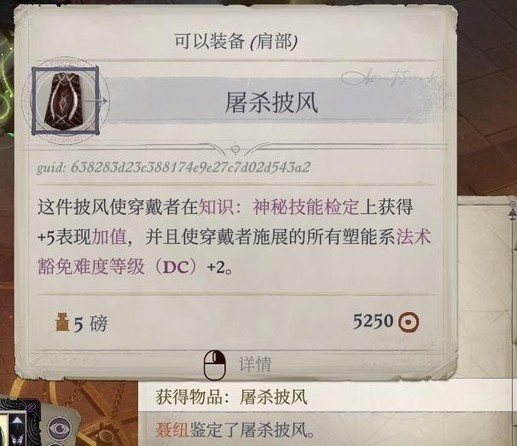
岛12最后的小boss还是扒了buff再打,有什么辅助都可以交了,打完出去休息一下,就到最后一个岛打第三章dlc3的boss了。战利品如图

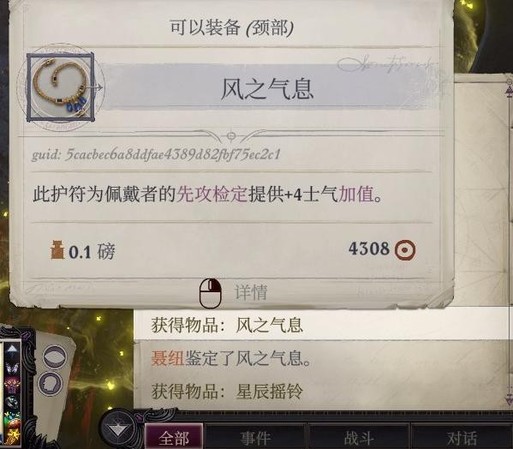
岛13星辰摇铃,血量降低后会变出分身,快速用范围法术打掉就好。打完获得残缺诡术师,我给席拉了。同时全队升15级了

15级
主角:博学士,高等元素专攻(火),游荡者-野兔魔宠,恶意变形术,地狱烈焰射线,伟岸雄姿
席拉:猛击终结
兰恩:精通先攻,集中猛击
聂纽:伏击施法,牧师-颂圣之语,可怖外表,阳炎爆
索希尔:超魔-甄选(为了甄选颂圣之语,对不起我太习惯用颂圣之语了
爱露:包抄、贴身射击
茶:技能专攻-世界(准备进博学士
狗:精通重击-匕首,天使之貌,维生气泡
烬:反正不带,随便点的(
鸟:突变斗士,精通重击-爪抓,高等武器专攻-爪抓
岱:精通先攻,战地医师,专精-颂圣之语(虽然目前还用不了但是为16级做准备),复活亡者,高等解除魔法,复生术
葛雷博的14级点了突变斗士-盾牌大师,当时还没想好给他用什么武器(手斧和卫士战斧的重击范围都不太行)所以没加15级的点
记得进第四章之前买钻石尘,移除状态卷轴(以及其他支援/buff型卷轴)和制作卷轴的材料
第三章收尾
圣教军那边极恶毒灵做了癫狂灾瘟给主角用

在指挥室跳过时间直到触发新的事件,接到米亚米尔任务,到冬阳村
米亚米尔任务,提前上共用防寒+抗寒,它第一轮放极地午夜第二轮放瘟疫风暴,所以我直接把正义烙印和炉台守卫都交了,第二轮不让它出手就杀掉了
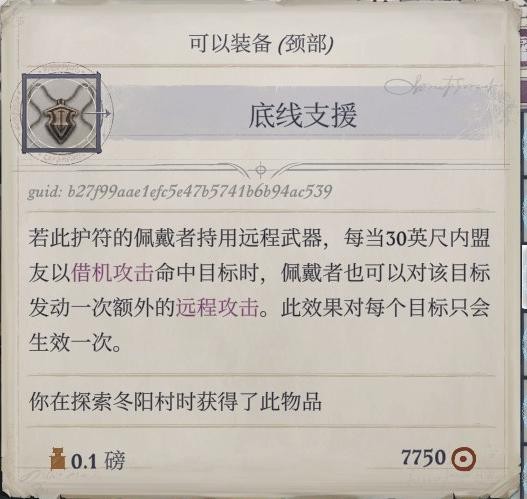
打冬阳村最难打的那个树人之前,。树人那边,现在等级高了,命中和伤害溢出就很好打了,两回合里主角四个火球术+兰恩砍几刀就没了(如果觉得不好打,可以让主角提前换上一下黑暗预兆,戒指给的疲乏波超魔之后可以留在法表里,对树人使用,它疲劳之后就不能使用闯越了),打完这边还有最后一个立石,调查完之后去石之心拿奖励(底线支援,给爱露)
冬阳村拿黄铜鞭后触发的幽灵,初始面板如图,对15级队伍来说不难打。会在地图各处出现,一共7次,彻底打完之后回到鬼魂的墓,获得19000+经验


这下真的只需要不断休息做卷轴等女王来了。来之后调整法术位+叠两种餐食加值然后打午夜神庙。
在灵使道途商人那里买的九环卷轴可以给聂纽学了然后做更多
当前经验685827,金币372869(花了很多钱买九环卷轴制造工具、钻石尘、钻石、恐龙骨头和buff类卷轴,因为第四章遇到说书人之前都没地方买施法材料,其中钻石尘不是必需,因为午夜庙宇隐藏房间打赢了也会给)
午夜庙宇
高难度下午夜庙宇比较麻烦的一点是刚进门就直接触发战斗,没有机会上buff。灵使/巫妖道途的指挥官可以先到灵使花园/巫妖塔,上好分钟级buff,再回要塞和女王对话开始战斗。其他道途我就不知道了,或许只能边打边上buff+拼运气吧。
另外敌人初始仇恨在主角身上,最好镜影术移位术都给主角上一下。
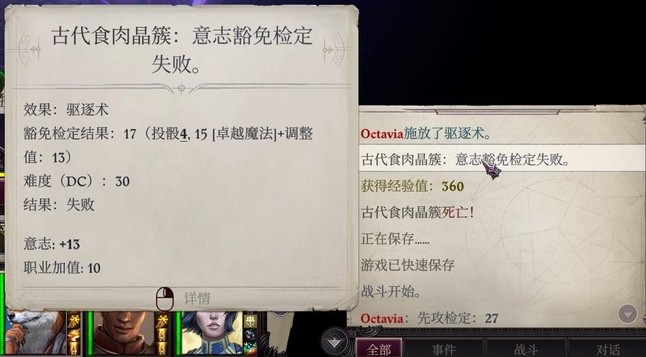
路线挺单一的,第一次下深渊之前的地图是这样。下深渊之后有食肉晶簇,主角可以用驱逐术秒杀

这边打小怪的时候主角和聂纽一般都是不出手的,输出就靠兰恩+爱露+用了祝福武器的席拉,主角和聂纽一般就是遇到比较难对付的怪再有针对性地控一控,压力实在大担心扛不住的时候主角扔个火球术(比如刚进门敌人仇恨都在主角身上的时候
第一次下深渊彻底探索之后的地图如图。主要战利品:(烈焰风暴和津波卷轴之后打隐藏房间的虫群或许有用


再上楼,遇到巴弗灭的仆从并触发第一次号角声。
这次探索完是这样,战利品如图。庙宇下层敌人会放火球术,注意防护

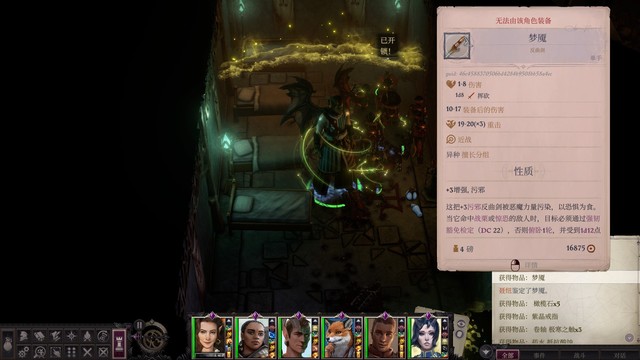
下来之后的这个房间有隐形的敌人还有陷阱,比较麻烦,可以爱露隐形过去拆陷阱,远程优先杀会放腐烂幻象的遁影魔信徒

再往前遇到真扬妮,辉光又升级了

接着遇到诺提库拉女祭司,对话,再往前的敌人会放心灵迷雾+群控,有点麻烦,空奢魔弱强韧,聂纽可以用刺耳尖啸+dlc3给的低等顽强超魔权杖控。这次清完怪后战利品和地图是这样
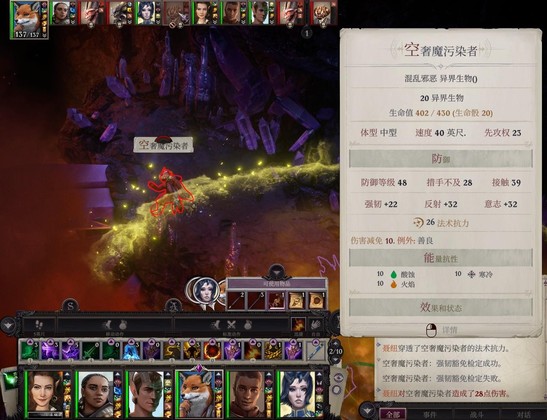

上来之后又触发第二次号角,之后出现的暴怖魔的初始仇恨又都在主角身上,注意防护和控制
前面这个房间内的敌人会放群体寒冰法术,还有虫群,提前做好准备(共用防箭+克集群吊坠+共用防寒抗寒)。爱露先进去拆陷阱,祭司可以让聂纽用甄选酷热之风控,主角火球术打虫群

打完这里就已经集齐三把钥匙,可以打午夜神庙的boss了,我先打boss再根据情况决定要不要休息一下再打其他怪
敌人会放剑刃障壁比较烦,开局只有席拉进房间触发剧情,其他人在门外拐角处待机,这样触发剧情后敌人第一轮就不会放剑刃障壁。
主角第一轮瞬发甄选酷热之风控住后面的妄乱魔信徒,聂纽补一发群体定身他人,索希尔上炉台守卫、席拉上正义烙印、爱露上狩猎目标,兰恩就可以稳定命中boss了。注意快要打死boss的时候抬高全队血量,同归炎爆的100火焰伤害+100污邪伤害可不是闹着玩的
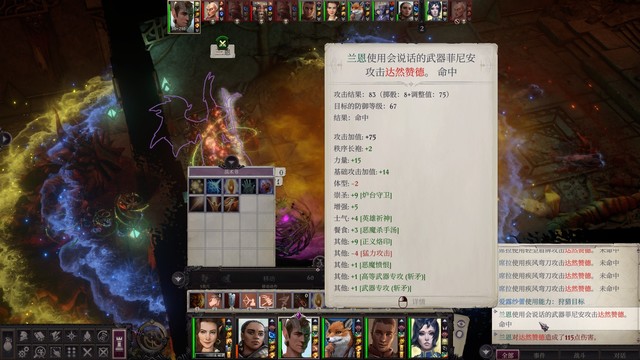
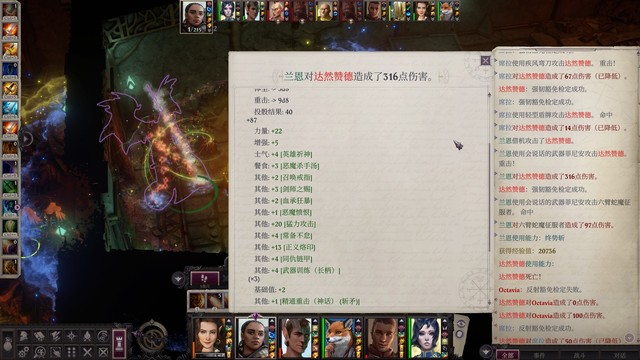 打完获得弯刀火风暴,给席拉
打完获得弯刀火风暴,给席拉
 之前在灵使花园上的分钟级buff也刚好掉光了,那就休息一下再打其他小怪吧,下次再玩
之前在灵使花园上的分钟级buff也刚好掉光了,那就休息一下再打其他小怪吧,下次再玩
休息后先把谜中之谜成就的隐藏房间打了(怎么开可以查攻略),下去之后首先过dc51的察觉,检定失败务必读档,解除陷阱(dc54)失败也务必读档(拆陷阱就给好多经验啊……),然后捡东西触发虫群*4


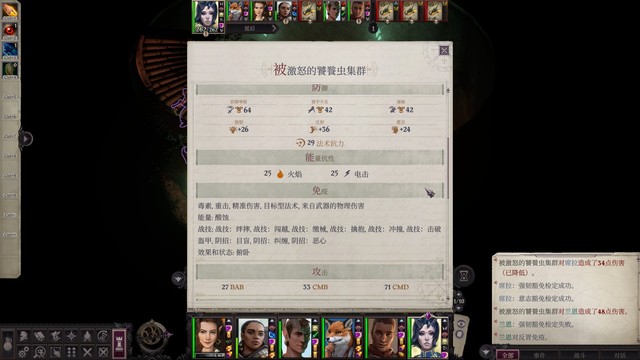 现在有dlc4的集群克星搭扣就舒服很多,还有主角的巅峰元素火……还记得我第一次玩核心难度的时候还没有带小烬,没人扔火球术,好像是靠前面恶魔掉的津波卷轴sl无数次杀掉的……总之主角和兰恩依旧是输出的大头,打打就过了……主要战利品如图
现在有dlc4的集群克星搭扣就舒服很多,还有主角的巅峰元素火……还记得我第一次玩核心难度的时候还没有带小烬,没人扔火球术,好像是靠前面恶魔掉的津波卷轴sl无数次杀掉的……总之主角和兰恩依旧是输出的大头,打打就过了……主要战利品如图
 没有dlc4的可以先打取乐的黑暗,打完获得一个集群克星搭扣给兰恩
没有dlc4的可以先打取乐的黑暗,打完获得一个集群克星搭扣给兰恩
接下来这个地方的射手比较多ab比较高,可以考虑用掉黑暗罩纱

再往前再次进入深渊,进入之前确保全队有防死结界(之前路过的德斯卡瑞雕像旁边有隐藏门,我打算下次休息之后再打),下去就触发和一大群不死生物小怪的战斗
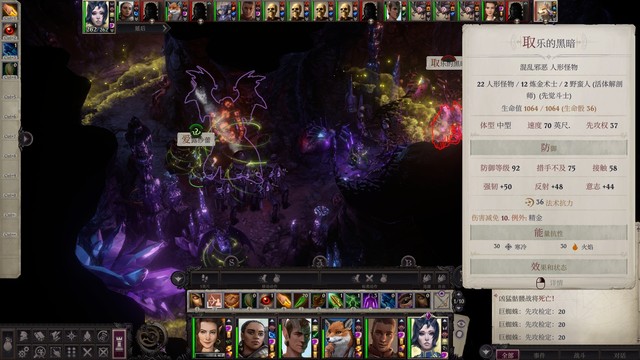
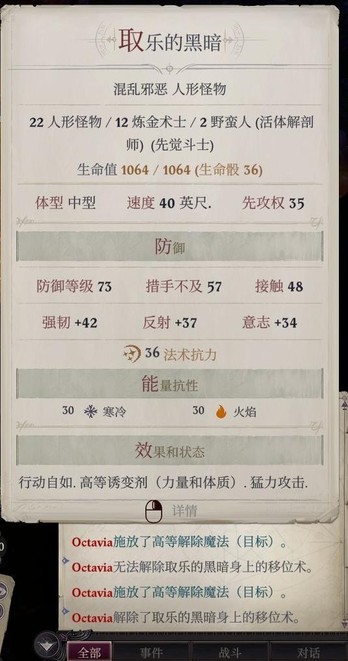
不公平难度取乐的黑暗面板如图,变态啊
 总之开战之前能上的buff都上了,炉台守卫我前面用掉了不然我这里一定会上,索希尔在取乐的黑暗那边召唤骷髅开战,这样它前两三局会先挠骷髅(和阴影宽恕给的巨蜘蛛,只要骷髅死亡就会出现)
总之开战之前能上的buff都上了,炉台守卫我前面用掉了不然我这里一定会上,索希尔在取乐的黑暗那边召唤骷髅开战,这样它前两三局会先挠骷髅(和阴影宽恕给的巨蜘蛛,只要骷髅死亡就会出现)

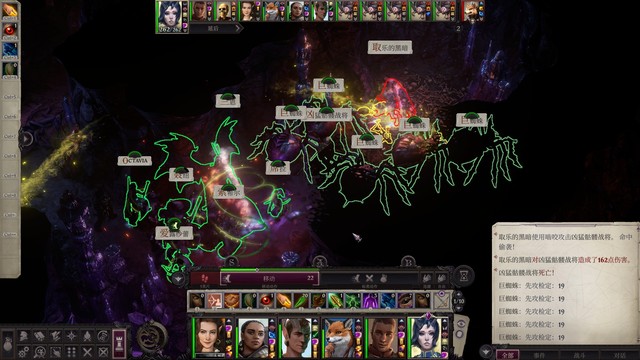 索希尔和主角使用解除魔法,解到最后是下图p1这个情况(此时它才刚刚把召唤物全杀光,走到席拉面前),此时兰恩搭配索希尔的领域辅助就可以命中了,席拉用屹立不倒顶住就好(主角还可以扔正义烙印加持下的魔法飞弹),这之后两回合就杀掉了,获得经验52224,又快要升16级了
索希尔和主角使用解除魔法,解到最后是下图p1这个情况(此时它才刚刚把召唤物全杀光,走到席拉面前),此时兰恩搭配索希尔的领域辅助就可以命中了,席拉用屹立不倒顶住就好(主角还可以扔正义烙印加持下的魔法飞弹),这之后两回合就杀掉了,获得经验52224,又快要升16级了
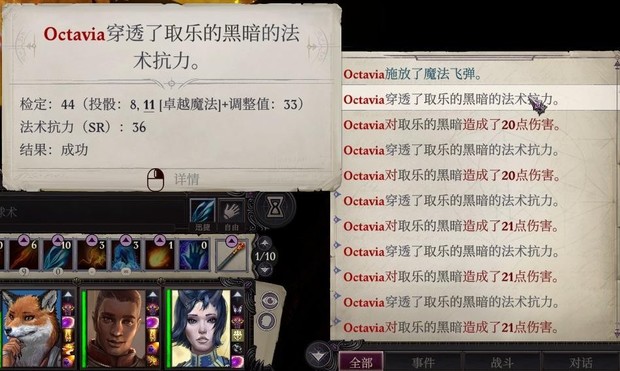
两回合内打完的具体情况:(前面还有巨蜘蛛roll出大成功打了几十血)



打赢的战利品
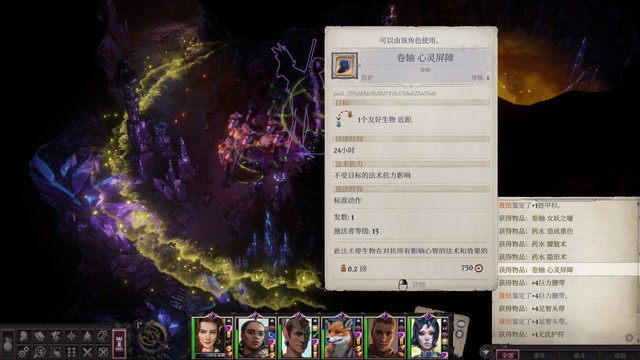
回去之前德斯卡瑞雕像旁边的隐藏房间,检定成功打完后里面是这样
可以进第四章了!
第四章
第四章要买的东西
奴隶市场
快速应敌护符(爱露
暴力呼召(+兰恩伤害,谁装备位空着就给谁
魅影向导(+3幻术cl,给聂纽
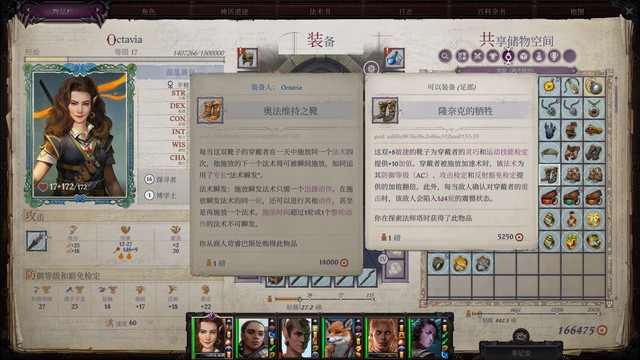
奥法维持之靴(主角
临危之戒(兰恩
高等瞬发/极效/强效超魔权杖(权杖永远不嫌多
拦截者(+5细剑,山茶
夜空闪(+5先攻的穿甲剑,适合席拉,如果席拉能点出穿甲剑相关专长就买给她
也有用但是我不买的
褴褛黑衫(以前给小烬,现在我不带就不买了
恶念僧袍(以前给兼职武僧的雷吉尔的,现在我不带雷吉尔
慑人巨力(不确定买不买,再看看
以及奴隶买了加手哥好感(
每把一个人那里的东西买完就直接开战杀掉,拿到传送金币、拿回买奴隶的钱,也免得后面灵使任务屠市场难打
还有屠光之后拿到的斩矛(菲尼安终于能下班了,不过还是找个人继续拿着,免得不能触发对话
万乐园
奸徒眼镜(+10察觉+10巧手
蜥蜴尾(动物伙伴
说书人
冰系扩表戒指(主角
善念僧袍(席拉
延时超魔权杖
重威之势和适时援助我不太用,买了备着吧
沃尔吉夫
神圣护卫卷腹(+4全豁免
神话5+16级+下城区初步探索
进第四章之后马上:
神话5
主角:第二血承-火元素
席拉:无穷辟邪斩
兰恩:屹立不倒
聂纽:高等充裕施法
索希尔:奇迹领域-崇高
爱露:分裂射击
之后记得打开主角的能量伤害转火伤害开关、给聂纽填充法术书
刚进第四章的经验是这样,进城逛了逛过了几个检定就16级了

16级
主角:探寻者,法术专攻-防护(主要是为了高等解除魔法),高等咆哮术
席拉:圣武士
兰恩:突变斗士,枕戈待旦,武器训练-长柄
聂纽:博学士,水幕拒敌,高等天使之貌
索希尔:牧师
爱露:谍报专家,杀戮型恶魔,魔法型恶魔
其他队友加点
茶:精魂猎手,巫术-秘咒-法术延时,高等武器专攻-细剑。变化自如
狗:奥法暴徒,野兔魔宠,战法转换,高等英雄气概。屹立不倒
鸟:突变斗士。屹立不倒
岱:先知,秩序护盾。偏好超魔-甄选(点之前先把颂圣之语超魔到8环,这样7/8环都能放了
在纽系营矿井获得运动技能检定加值加冲锋伤害的靴子,我给兰恩了
和佐格斯与他妈对话,把佐格斯接到营地加手哥评价(第四章末和最终战也可以帮忙打一打)
进入烂肠坑,获得凶兽急袭(+4短弓,让使用者的动物伙伴永久处于加速术状态下,对我来说没用我就卖掉了)
到酒馆和面熟的人对话获得灰烬制造者(我给主角了,战斗法师木棍换下来给聂纽),和老板对话付500金币问传闻,获得酒馆传送金币,顺便卖一下打午夜庙宇的战利品,我卖完包里有58w+(只卖了普通装备,还有好多有特殊名字的装备没卖,之后卖给沃尔吉夫)
接下来打算多带一阵子岱兰试试了,索希尔下个班。配队就是老四位+岱狗,岱没学的共用石肤狗正好会,狗还能帮岱上上共用抵抗/防护能量的buff(因为没给岱点三充裕),而且岱虽然没有索希尔的领域能力,但我之前给他点了双持久,在第四章逛街打小怪应该还是挺省心的。以及既然带了岱,聂纽可以记一个动物异变了,正好五环现在没什么好记的(冰牢都顽强超魔到7环去了)
在第四章这边只记一份buff就够了,持续以及已经挺长了,掉了就回营地休息
把其他用不着的武器卖给沃尔吉夫了,当前金币71w+
传送回营地,看岱兰恋爱剧情,休息了一下,和队友对话,爱乌升到20级学会1环2环法术了,神圣恩典可以时不时用一用
带上小队重新出门到下城区,在dlc3商人处花九万买了大型次元袋
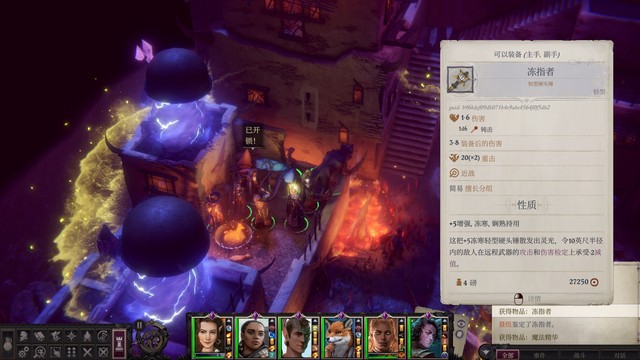
在下城区通过次元门拿到的装备:
酒馆的某个门口遇到冥娜蛊雇来的杀手,威吓检定成功就不用战斗,得知冥娜蛊的藏身处
遇到小烬和恶魔布道,接受小烬任务
城里的运动检定都可以过一过,经验不拿白不拿(到了中城区我就先爬回来了,不着急上去)。墙上的宗教检定一定要sl过一下,关系到深渊阴谋成就
逛街还拿到:
- 第四章逛街有一个小技巧是,路上名字是市民/乞丐/奴隶这种的一般不会攻击主角,名字是怪物名的一般会在主角靠近/互动之后敌对
在这个位置触发第一场战斗,有食魂魔和爆燃魔,记得上防死结界和共用防火。后面刷出来的魅魔会上群体困惑,主角可以先手控一下

进入冥娜蛊藏身处,再次战斗,我让聂纽用甄选酷热之风控了一下,冥娜蛊不难打,如果难命中就上个正义烙印,主角可以针对性控控对面会上群控的小怪
打完我选了灵使道途选项放冥娜蛊走

在这里触发第二次战斗,难度是白给,打完获得神射手
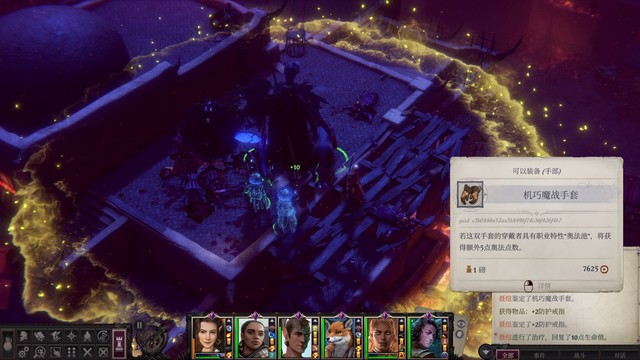
传送上来到这个位置,触发第三场战斗(有炼金术士的位置),打完获得机巧魔战手套,传送到更靠南边的平台还有星刃
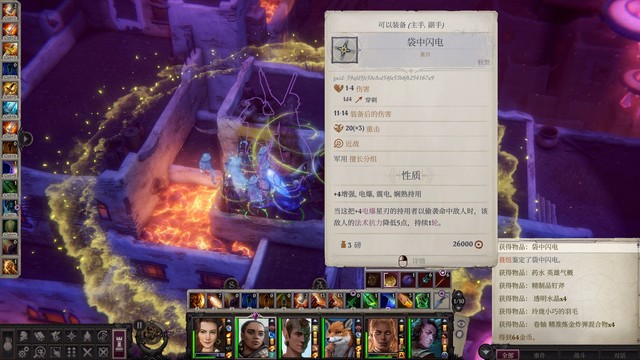
(风暴束是神……然后再瞬发一个火球术,主角现在就是一个法术炮台……)

这个位置也有战斗,初始数值见p3,敌人都弱强韧,灵魂猎手难命中的话可以挂个正义烙印/主角用个高等解除魔法,打完获得腰带

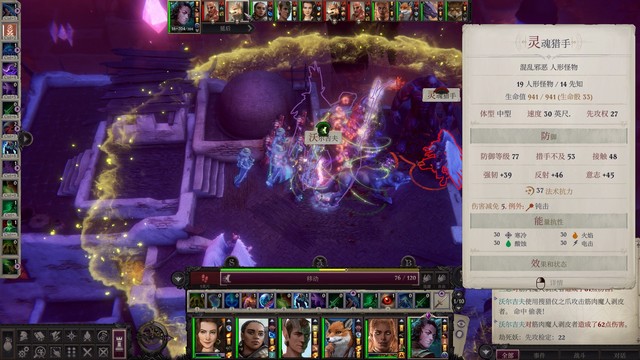
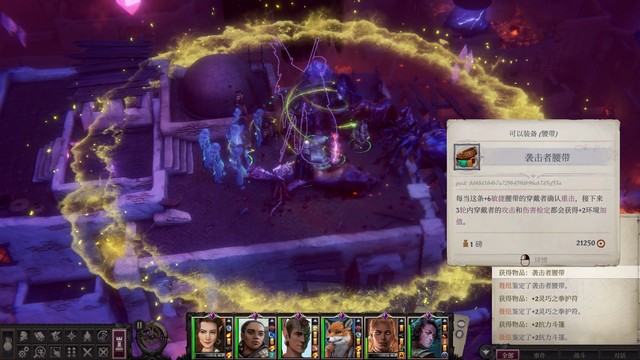
这些应该就是下城区街道上目前能遇到的所有战斗了,去角斗场,如果法术用完了也没关系,一会儿恶魔移植可以恢复法术位
到角斗场(带着聂纽),和医师对话,给聂纽做手术,然后再给主角做(手术效果如图

进角斗场对话后打第一场战斗,对手是一群火魔蝠,没难度,可以上个共用防火但我觉得连这都没必要。打完回去再次对话,获得战斗极乐金币
对话说要打下一场,被要求找奴隶来,我这里先接了任务。
出门到地图左下角和高阶守卫对话,过威吓检定,可以进中城区了
中城区+角斗场任务+莎米拉任务
进中城区之后往前走两步就触发战斗,主角一个风暴束就几乎全控住了,砍砍就过了。没记错的话小头目好像是会扔带火焰伤害(还是酸蚀?)的炼金炸弹的,可以防一下
前往活畜市场,先逛一圈对对话买买东西,中间还会触发缝线的剧情(买下缝线),没有准备的时候最好先不要挑起战斗
我给了冒险队长钱,为了手哥好感(其实只差这点应该也是无所谓的)。还获得了希洛的信,解锁了希洛的任务
还解锁了无畏的调情任务
黑假面处购入夜空闪(席拉)、拦截者(山茶)、慑人巨力(岱兰的狼/爱乌)、嗜血腰带(最后这个纯粹是我一时起意买给狗),买下角斗士,让他们去纽系营
买过黑假面的装备和奴隶之后就可以和黑假面对话开战了,怕一轮打不死/控不住可以提前上个共用防护能量(我遇到的是酸),他会用群控+炼金炸弹,战后获得奴隶市场金币+拿回买奴隶的钱
苛xxx的奴隶不要买,信手哥准没错,装备可以买奥法维持之靴(主角)、临危之戒(兰恩)、魅影向导(聂纽),以及各种权杖。
走之前还把拉基的奴隶和魔蝠都买了,魔蝠涉及到某个战斗成就,还卖不用的装备凑出最后一点钱买了他的快速迎敌护符(爱露)和暴力呼召(随便谁反正带着就行),打算之后把拉基杀了他死掉的时候会释放火焰伤害,注意防护。
没忍住把代安克的奴隶也买了、让他们去纽系营,然后把它也杀了,它可能会优先攻击主角,同样注意防护,它ac比较高,同样可以高等解除魔法/交正义烙印(其实可以在开战之前就扒它身上的buff,只不过扒掉的buff读档之后会再次出现)
奴隶市场就先逛到这里,分钟级buff差不多掉完了,去酒馆做完无畏的调情任务然后回营地休息一下顺便接队友任务,然后再传送到角斗场,进去打第二场战斗
角斗场打第二场战斗,敌人弱强韧,咆哮术控。出来对话,被要求找魅魔过来,我不找了直接打(过交涉骗到四万块
打第三场战斗,挺好打的兰恩第一回合就砍死了,触发剧情,被带到角斗场后台,打歌xxx之前探索一下和所有npc对话,然后打歌xxxx。两波小怪后歌xxx出现,弱强韧,咆哮术控。打完看完剧情,角斗场这边目前就基本没什么要做的事了
传送回到奴隶市场,继续探索
这种机关,每放平一个平台就让一个队友过去踩着,尽头是奖励
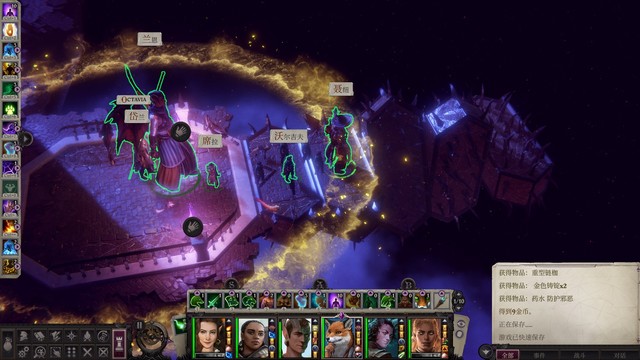
进入情热幻梦寝宫,找莎米拉寻求庇护,接任务。先不去做任务,继续探索中城区,触发神裔事件,接任务对付红面具
再往前,在墙上sl过宗教检定
然后从p1位置上去,向上传送在p2这里打魔孽,只要席拉能t稳就不难打,打完获得泰坦符文


旁边是万乐园,进去对话接琪瓦罗和蜜语xxx的任务
从万乐园后门前往上城区,出来打一群牛头人,再从这里过灵巧下去做蜜语xxx任务(旁边的房间里获得生命传导者
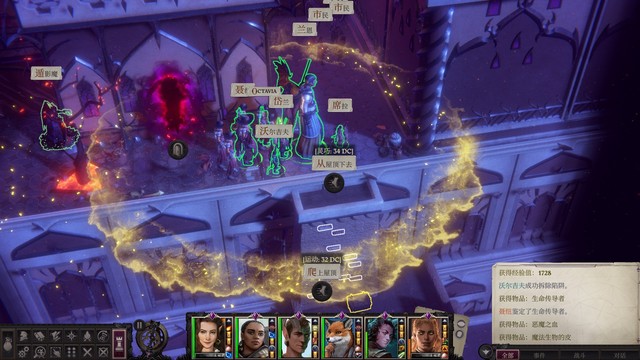

继续下来和这两群恶魔战斗(第二群打之前忘截图了),先不要上去(会触发爱乌绑架事件),先去万乐园继续蜜语xxx任务


看完蜜语xxx任务获得永恒歌谣,从这里往下传送,又打一群恶魔,然后中城区就差不多逛完了,到下城区1打烂肠坑2做莎米拉任务找齐xx
到下城区和这个乞丐对话推进任务

烂肠坑旁边出现了一群火蜥蜴,打一下。然后进烂肠坑,进去就触发战斗,风暴束控一下再随便打就过了,打完推进冥娜蛊任务

接下来在这里和乞丐对话推进任务
然后在这里看到一大群乞丐,得知齐xx下落。找到齐xx对话,接下来要去上城区法师塔,先不去

回万乐园和琪瓦罗对话,灵使道途可以告诉她冥娜蛊被放走了,其他道途下她会跑出去,在下城区一大群奴隶的位置等着和主角战斗。
出万乐园大门再进去,和万乐园的新主人对话,获得万乐园传送金币,传送去酒馆和红面具对话,再传送回营地休息、接队友任务
上城区+17级+队友任务+灵使任务
休息完传送到万乐园,走后门到上城区,到破碎狂欢门口和旁边的致命xxx战斗,打完进去接约会任务。
出来,向上传送,和神话妄乱魔刺客战斗,弱意志,用群体定身他人控(对着队友放,可以控到非人生物)。再往下,打警惕的阴谋家和周围的射手,注意上防死结界。
继续往前,直接触发对话进入兰恩任务地点,剧情后战斗,感觉多用几个群体法术就没难度,小心陷阱。
打完捡捡东西出来,打这群恶魔,这样这片区域就基本上清理干净了(附近的平台传送上去可以获得眼镜和待修复物品
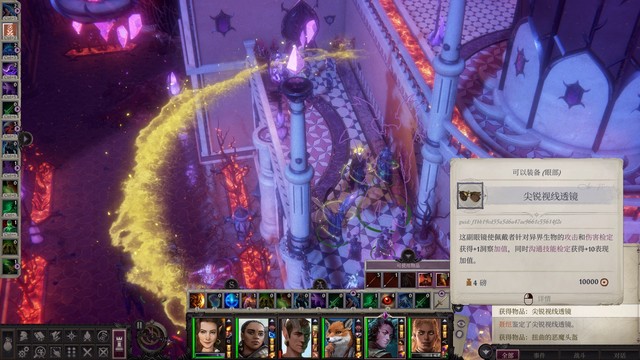
接下来回到上城区门口的广场,在p1这里向下传送,找到废弃宅邸p2做沃尔吉夫任务
沃提尔很好打
然后打外公,只有图中这个是真身,ac比较高,可以高等解除魔法+正义烙印,然后我出了重击连锁直接打死了
 打完看完剧情再逛一下房间,我让沃尔吉夫拒绝力量,捡到了招摇撞骗
打完看完剧情再逛一下房间,我让沃尔吉夫拒绝力量,捡到了招摇撞骗
出门,打冷酷暴君,打死会放火焰aoe,注意防护。
 我打完打累了不想打了,去把约会任务做完获得传送金币、维勒西亚的调节护符(给主角)和大量经验。
我打完打累了不想打了,去把约会任务做完获得传送金币、维勒西亚的调节护符(给主角)和大量经验。
17级
主角 暴力解法 专精-高等解除魔法 火焰烙印 可怖外表
席拉 突变斗士 擅长异种武器-穿甲剑 精通重击-穿甲剑(换上夜空闪(之后差不多就一直用这个了,主要是为了+5先攻
兰恩 突变斗士 武器专精-斩矛 高等武器专精-斩矛
聂纽 博学士 法术专攻-惑控 德鲁伊法术-树肤(从此爱露/山茶/岱兰不再是队伍必需了……!) 神威如岳 诡影杀手
岱兰 先知 法术专攻-防护 法术专精-颂圣之语 迷醉波 高等天使之貌
小狗 高等双武器战斗 剩下的法术我都不太用所以随便点了
到宠妃看台,走侧边的桥,又是图示恶魔群。打完在旁边乱伦宫殿捡垃圾。再往前吸血鬼xxx的ab还挺高,我先不招惹,先去法师塔,拆拆陷阱打打魔像解解谜(还能拿到一点装备,还有个+5致命导体匕首可以给小狗)最终能遇到说书人,对话,缺什么可以买一下,我先不买了,以后还会来

 其实还没休息,现在顺便在法师塔休息一下好了……!休息完出法师塔,把旁边的吸血鬼xxx打一下(上防死结界和黑暗罩纱
其实还没休息,现在顺便在法师塔休息一下好了……!休息完出法师塔,把旁边的吸血鬼xxx打一下(上防死结界和黑暗罩纱
旁边调整平台拿到信仰承载者
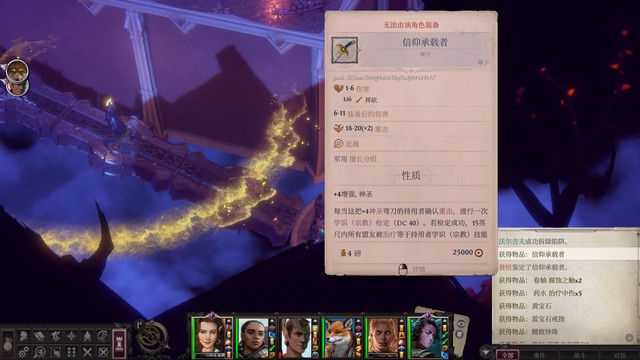
旁边向上传送后到达的平台,再次sl过宗教检定
回到宠妃看台,传送回营地,去矿区拿水晶(此时意识到忘了买酷寒之力戒指,拐回去找说书人买,让主角能用寒冰之躯。顺便修复了物品,获得的装备如图:
 可以根据需要选择,其中斗篷的效果会根据道途有所不同。我选的是靴子,给了小狗),只带会寒冰之躯的队友(我这边就是主角和聂纽),用上寒冰之躯免疫食肉晶簇的控制效果然后法术轰炸,比带上所有队友更好打。
可以根据需要选择,其中斗篷的效果会根据道途有所不同。我选的是靴子,给了小狗),只带会寒冰之躯的队友(我这边就是主角和聂纽),用上寒冰之躯免疫食肉晶簇的控制效果然后法术轰炸,比带上所有队友更好打。
想起来红面具任务还没做完,本来打算找莎米拉交任务的时候做,但是怕到时候buff掉了,所以先传送过去做一下。也不难打,同样是高等解除魔法+正义烙印然后就随便打,而且弱意志,可以控
接下来做一下队友任务(索希尔、葛雷博、爱露),所以给这三位升一下级+调整法术位,然后再出发
升级加点
索希尔 牧师 法术专攻-防护
葛雷博 15突变斗士 精通重击-弯刀(用席拉换下来的火风暴) 武器训练-重刃 16野蛮人-先觉斗士 17受诅巫师 精通先攻 野兔冻皮跛足 神话5无限狂暴
爱露 谍报专家 额外演艺
记得把装备换上,这次带主角席拉聂纽索希尔爱露葛雷博
传送去宠妃看台,回法师塔找说书人推进任务,再去莎米拉那里继续推任务,获得诺提库拉的邀请,可以见诺提库拉了,如果不想这么快离开手哥就先不去见,无所谓就可以见。这一路上都没有战斗,可以不上buff。
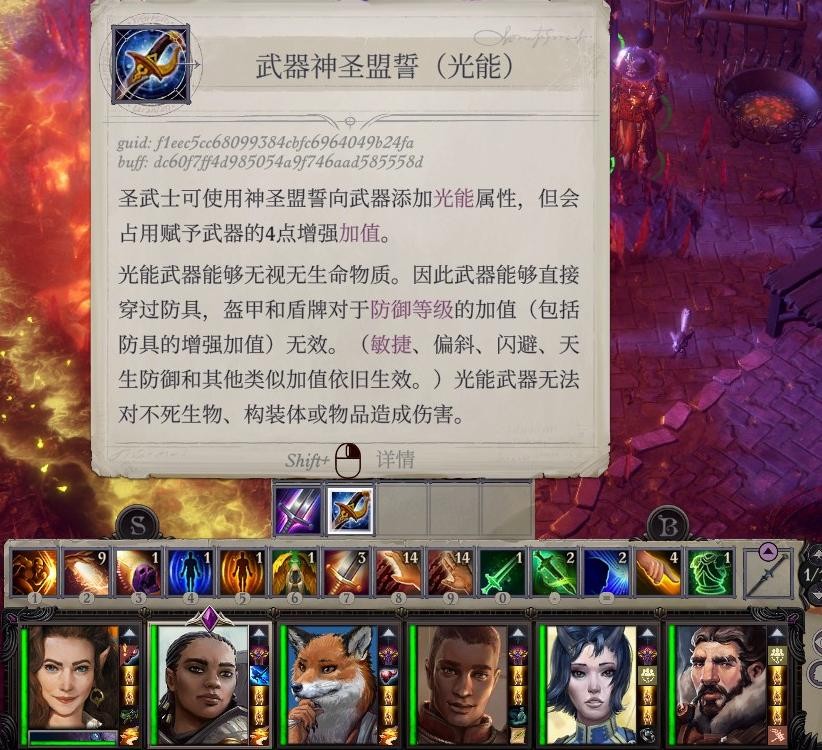
我还在说书人那里购入了善念僧袍给席拉、适时援助和重威之势备用,之前拿到的焦黑屏障可以给席拉换上了,换下来的盾可以给葛雷博,葛雷博拿着的卫士盾牌就可以卖掉了。以及席拉现在有光能武器了,可以开一开
到战斗极乐做索希尔任务,看剧情就好
回到奴隶市场,购入所有想要的装备和道具之后上buff杀了苛xxx,这样还没杀的就只剩中间那个市场老大了。到从中城区前往上城区的门,触发爱乌被绑架事件,顺着提示做任务就好,第一次战斗比较简单,第二次是屠奴隶市场,相对难一些,索希尔席拉爱露的辅助能力都可以用
灵使道途屠奴隶市场这段还有这个buff

以及没注意什么时候有了自信之心法术了,有了就可以用,很好的buff
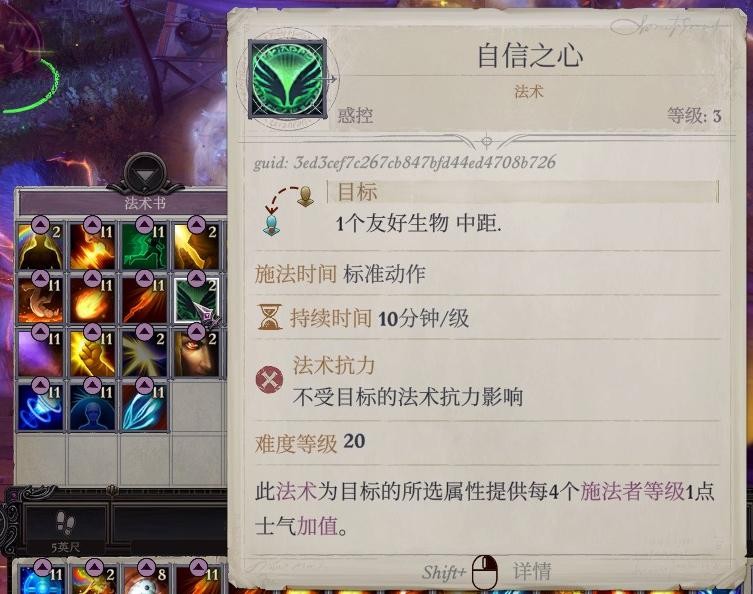
(现在有席拉、索希尔和爱露在,ab就没有叠不上去的)


做完灵使任务传送去宠妃看台,做爱露和葛雷博任务
到邪恶知识宝库,不断选择没有选过的门就可以了,之后触发战斗,不难打,打完陪葛雷博去刺客工会(在中城区,门需要特定角度才会出现,如图

到上城区入口大门处,爱露任务地点的门要爱露在队里才会出现。进入,剧情后战斗,同样不难打。最后回营地和队友对话就好。
情热幻梦那边出现了新的怪,可以去打一下,打完获得决心法袍,给主角换上
还把万乐园这边的好装备都买了,之前屠奴隶市场拿到的悲报传达者给兰恩。还有找说书人买一下延时超魔权杖
深渊阴谋+卑微的怪拟魔+推进主线+神话6
深渊阴谋成就和中城区挑战怪
按照下城区-中城区-上城区的顺序依次把之前拿到的泰坦符文放进之前过宗教检定的地方强化,放进去之后会触发战斗,三波怪,全部打完再拿出来进行下一步
下城区的在地图右下角,其中第二波怪会用心灵迷雾+群体困惑术,可以针对性准备一下
中城区的在变态神裔家旁边,不难打,中了阳炎爆的目盲可以用席拉的圣疗(前提是之前升级的时候选了圣疗可以治目盲),或者移除目盲,或者医疗术。
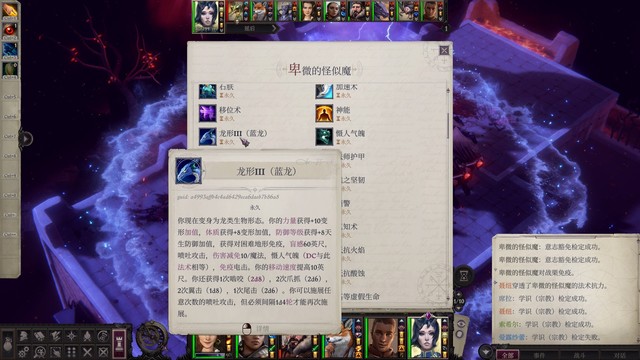
打完可以传送到神裔家楼上,顺便和卑微的xxx互动,打一下这里的挑战怪。
打之前全员覆盖防死结界和黑暗罩纱,卑微的xxx身上一堆buff,dc不高可以解除,但解除后下一阶段它还会重新上回来。第一阶段它会召唤3只食魂魔,第二阶段召唤5个魅魔弓箭手(我让聂纽用魅影杀手秒了3个),第三阶段它会变成龙(p1)。主角索希尔扒buff,聂纽前两轮控小怪后面摸鱼,席拉爱露葛雷博稍微触发个重击,很快就杀掉了(p2)。中了力竭波可以用席拉的圣疗解除
上城区的在这里,提前上抗酸防酸,主角多扔风暴束和链状闪电就好

彻底打完获得完美符文,我这里顺路去找说书人买了延时权杖、补充了一点卷轴,还复原了含羞百合头盔(给席拉,ac+2亵渎,不如袍泽头盔最高+3士气,但胜在稳定,而且送力量+4亵渎),然后回营地休息一下。
玩到这里发现忘做希洛任务了,去万乐园做一下

休息完传送去情热幻梦,放入符文出现门,进去是深渊阴谋的最后一场战斗。提前上黑暗罩纱。

弓箭手比较烦,房间内部还有操念使。可以开局传送过去,先杀操念使,注意不要触发房间内的陷阱,尽量卡视角,让弓箭手射不到后排,并且让索希尔放甄选剑刃障壁,利用小空间,敌人跑不掉只能吃伤害,主角放风暴束/链状闪电也会很爽
打完经验1713382/1800000,又快升18级了。
- 如果手哥出来帮忙次数太多,可能会被德斯卡瑞的回声发现:

这样第四章见诺缇库拉之前除了dlc3之外的内容就基本都打完了,可以去见诺缇库拉了。可以带上小烬,看完长剧情获得神话6,悖论秘典给不给都行,然后做山茶任务,带山茶去万乐园然后过剧情、自己做选择就好了
神话6
没说的点的都是精通先攻(除了雷吉尔、特雷弗和小烬我不带所以没继续加点
主角 灵动魔法
山茶(先点17博学士 精通先攻 法师法术-战法转换(现在有点后悔了想点识破命门,但懒得读档改了
兰恩 武器专攻
和女王对话还拿到了一些奖励(如图
 之后如果不考虑rp的话就坐女王的飞船去最保险。接下来我要做坏东西,把不需要的npc都杀掉了。
传送到厄运酒馆,杀米勒拉,获得两件惑控法装备,都可以给聂纽
奴隶市场的另一个船长不知道去哪了,那就不杀了。
休息一下,去dlc3了!
之后如果不考虑rp的话就坐女王的飞船去最保险。接下来我要做坏东西,把不需要的npc都杀掉了。
传送到厄运酒馆,杀米勒拉,获得两件惑控法装备,都可以给聂纽
奴隶市场的另一个船长不知道去哪了,那就不杀了。
休息一下,去dlc3了!
dlc3+18级+当前配装
具体怎么打就不仔细讲了,列一下dlc3的战利品
岛1(主角有了灵动魔法放链状闪电一个顶俩一键清屏所以不难打)

岛2(刚进门走两步就18级了)
18级
主角 探寻者 迷醉波 专精-高等解法 共用心灵屏障(聂纽放不了这个 我也懒得用卷轴 所以主角来)(另外在小狗那里买了神圣护卫卷腹给主角,+4全豁免的)
席拉 突变斗士 盾牌辟矢
葛雷博 杀手
聂纽 博学士 预警 群体冰封之牢
索希尔 牧师
爱露 谍报专家
山茶 博学士
兰恩 突变斗士 高等诱变剂
小贼 原职业 法术乱点的
鸟哥 17突变斗士 赋能野性变身 高等武器专精(爪抓) 18突变斗士 武器训练(天生)
岱兰 原职业 复仇旋风
小烬、特雷弗和雷吉尔,我两个不用、一个不会用,就不点了,第六章再升级都行


岛3
战利品除图中外还有一根高等瞬发



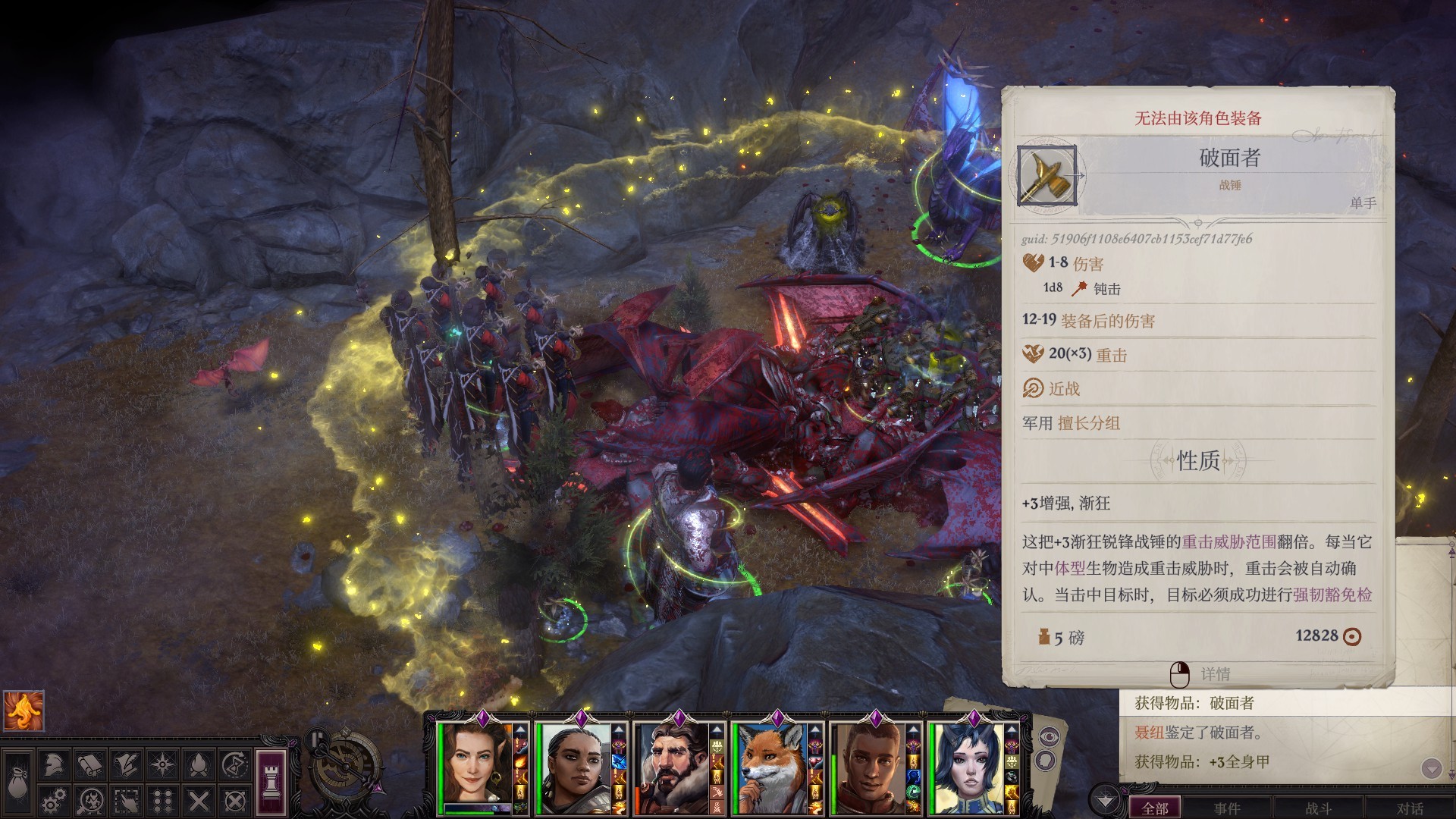
岛4
高奏凯歌戒指,士气加值翻倍,我给葛雷博了,可以让灵使道途给的自信之心(力量)+3士气加值变成+6,力量从43变成46,力量调整值从+16变成+18,ab再+4士气(高等英雄气概/英雄祈神),算下来一共就是ab+6
岛5(有食肉晶簇,备好驱逐术)

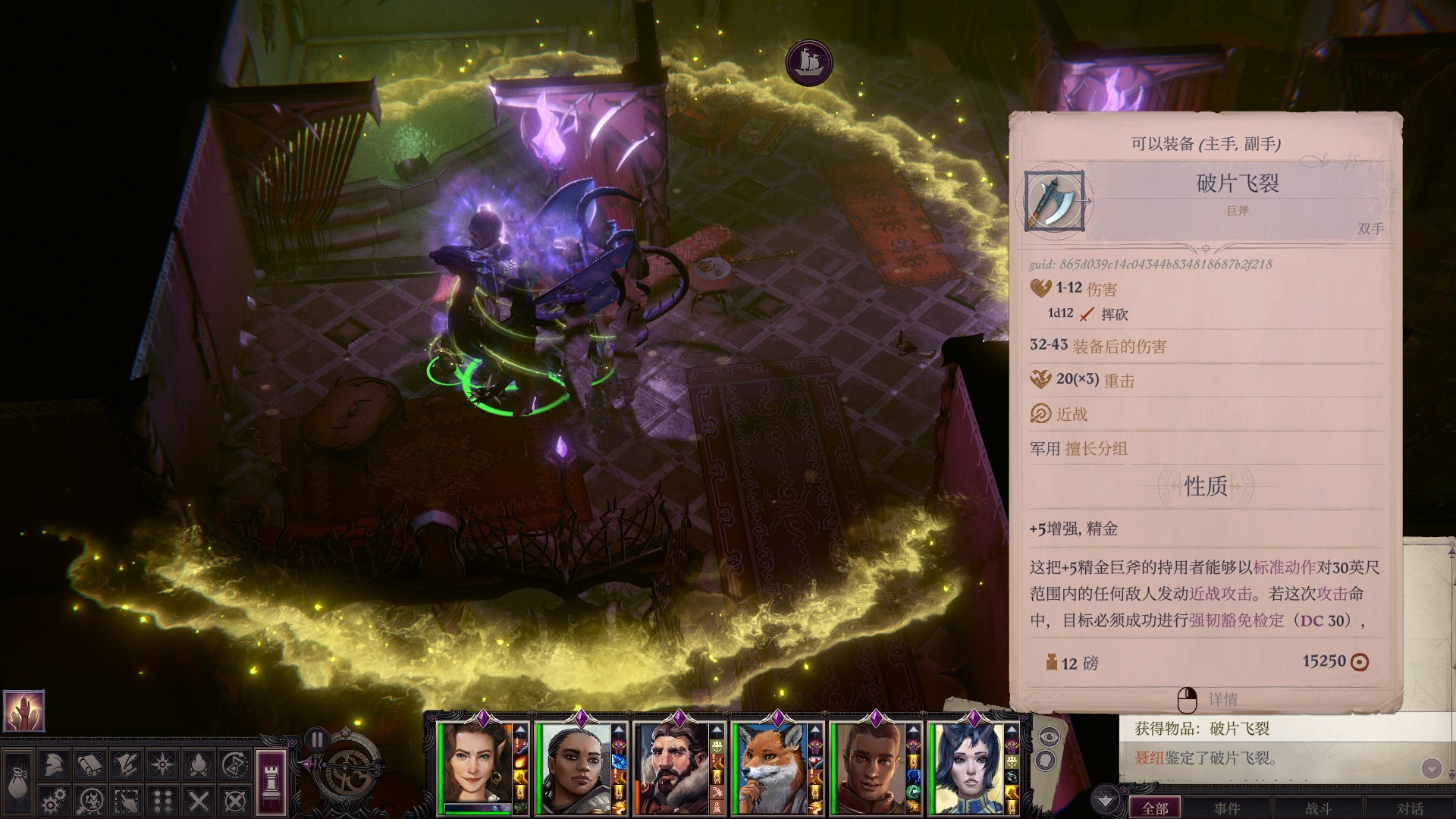
岛6(需要防死结界+共用防电)
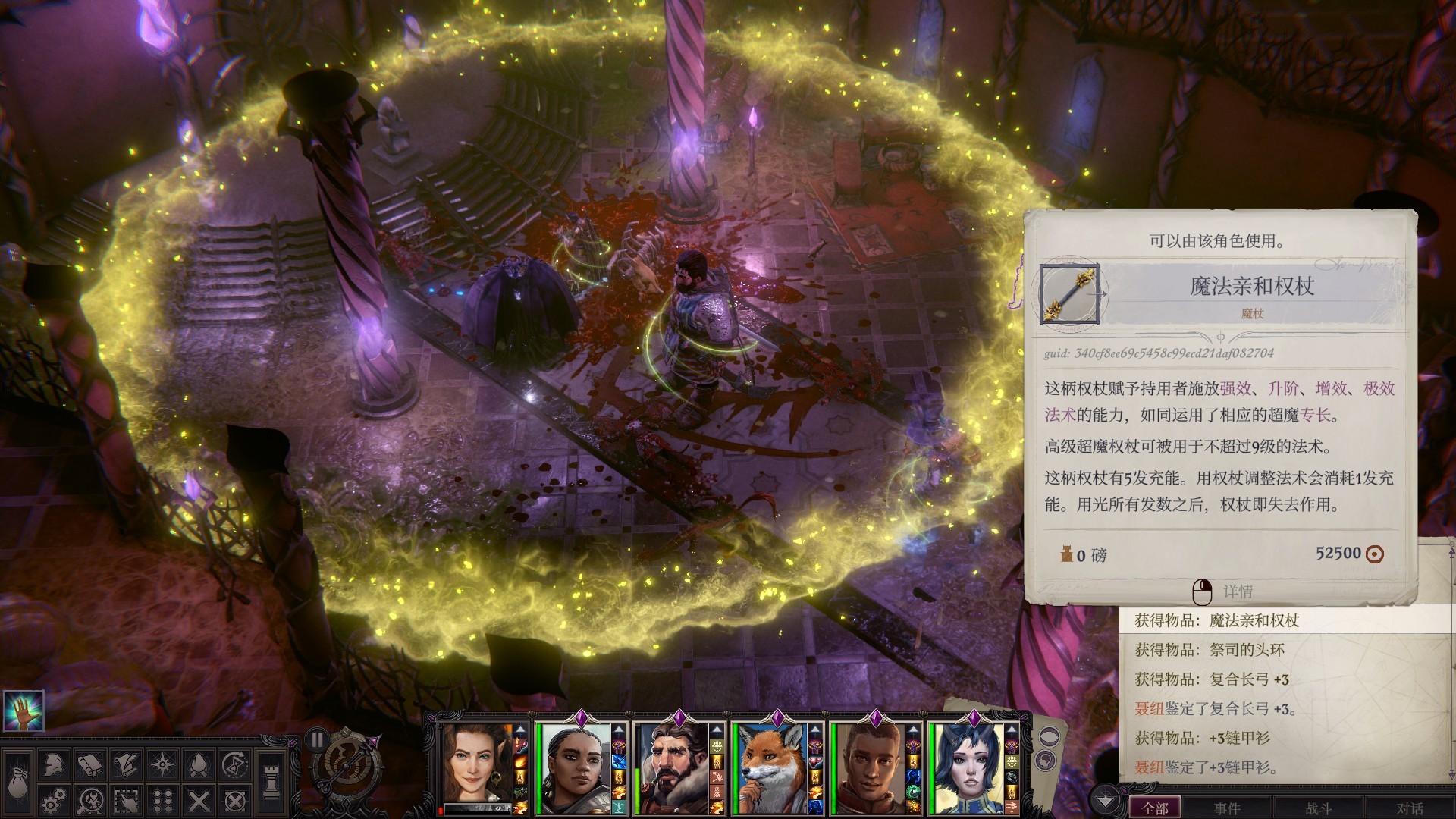
岛7(末尾又有回满状态的雕像,下次就可以直接去打dlc3第四章的boss了)
岛8
boss战,打身上有特效的小怪,提前上共用防寒,第二波敌人会用打强韧的法术,可以先手控一下。感觉这个boss战设计比较适合带远程来打。打完经验如图
 回去找说书人补充一下卷轴,再休息一下就去女王那坐飞船了,队伍是主角席拉兰恩聂纽爱露索希尔。这次不用叠餐食加值,因为反正会掉(
回去找说书人补充一下卷轴,再休息一下就去女王那坐飞船了,队伍是主角席拉兰恩聂纽爱露索希尔。这次不用叠餐食加值,因为反正会掉(
大家目前的装备
主角(当前无buff面板魅力36)(用了+2魅力书):
灰烬制造者(塑能cl+2,攻击检定+2,+4焰爆
备用:癫狂灾瘟(连续放三次同一个法术,下一个法术被强效+极效
重威之势(+6魅力,每天三次推开敌人
纯净视域眼镜(每天一次解除魔法大成功,法穿+1
屠杀披风(知识神秘+5,塑能dc+2
稳定之指(+2防护戒指,接触攻击检定+3
纵火狂之戒(火焰伤害额外+1d6+5,法穿+2
风暴领主的决意(给法表增加一系列电法术,还有电抗和反伤作为添头
维勒西亚的调节护符(天生防御+5,当前最高属性值+2
神圣护卫腹卷(+4ac,所有豁免+4崇圣
决心法袍(过强韧的法术dc+2,法穿+2,专注+4,法抗18
马兰德的耻辱(火焰法术+2d6污邪附伤,免疫火伤但弱冰和神圣
秘法根除手套(接触攻击检定+4,使用魔法装置+5表现
奥法维持之靴(一天内使用同一个法术四次,下一个法术就可以瞬发
旧魔典(+3一级法术位,+2二级法术位,+2三级法术位
高等强效超魔权杖
高等瞬发超魔权杖*2
高等极效超魔权杖
席拉
夜空闪(+5追击震电穿甲剑,+5先攻
焦黑屏障(+4重盾,免疫寒冷,对中小型敌人ac+1
含羞百合的头盔(力量+4亵渎,ac+2亵渎
残缺诡术师(感知和魅力+6,受到能量伤害获得一轮该伤害20抗性,受到物理伤害获得一轮减伤20
灰烬斗篷(+5抗力斗篷,每回合对10英尺内敌人造成2d8火焰伤害
霜护(ac+2,10点寒冷抗性
正义圣教军之戒(辟邪斩+1
重臂护腕(双持时副手武器伤害检定+3(搭配盾击
出双入对(和兰恩搭配,ac+2,攻击检定+2
虫壳甲(主要是为了ac,有敌人近战命中时反伤做添头
善念僧袍(对邪恶敌人ac+2,攻击检定+2表现
莎恩芮战裙(+2天生防御,灵巧+4表现
疾驰骑士的手套(攻击检定+1士气,没什么好手套了
脱缰之靴(永久行动自如
阿罗登之怒(辟邪斩的ac加值变为崇圣,每轮第一次攻击伤害+1d4神力
后继者圣契(30英尺内队友法穿+2,武器视为善良寒铁
黑暗罩纱(每天一次全队对远程攻击完全隐蔽
镜影术魔杖
兰恩
悲报传达者(+4残忍恶毒斩矛,每命中五次就可以多攻击一次
恶魔愤恨(狂暴时近战攻击检定、伤害检定、意志豁免+1
邪眼护目镜(察觉+10
嗅血斗篷(狂暴时对受伤敌人攻击检定+2
高奏凯歌戒指(ac+2偏斜,佩戴者所有士气加值翻倍
临危之戒(攻击和伤害检定+2表现,重击时敌人过dc26强韧豁免否则被击倒
猪突猛进护腕(力量+6
出双入对(同席拉
同仇链甲(夹击时对被夹击生物伤害加值+4
秩序僧袍(对混乱敌人攻击检定+2
袭击者腰带(+6敏捷,重击后三轮内攻击和伤害检定+2环境
剑师之赐(伤害加值+3,攻击检定+2
狂奔之靴(运动技能点作为加值加到冲锋时的伤害检定上
幸运骰子(每天一次,攻击检定+1或伤害检定+1或ac+1,持续全天
虎虎(察觉和自然+2士气
聂纽
魅影向导(幻术cl+3
德莱文的帽子(智力+2亵渎,可以瞬发加速术,每天一次任意法术瞬发
心灵大师之眼(惑控dc+2
屠杀披风(同主角
魔术师的戒指(幻术dc+2,使用魔法装置+5表现
斑斓炫目之戒(惑控dc+2
灼热护腕(塑能dc+2
明晰镜饰(影响心智dc+2
+3腹卷
七罪法袍(所有cl+3,dc+1,法穿+5
恶魔之影腰带(放6级及以上法术自动召唤遁影魔
缠惑手套(惑控dc+2,受此用法术影响敌人时对方意志-2持续3轮
精灵靴(灵巧+5,凑数的
全是魔杖:低等顽强、高等顽强、甄选、高等甄选、瞬发
索希尔
战斗法师木棍(dc+2,法穿+4
正能量经匣(引导能量治疗量+2d6
无可辩驳眼镜(先攻+2亵渎,永久真知术
暴力呼召(30英尺内狂暴队友攻击和伤害检定+2
阴影宽恕(所有队友每轮一次额外借机攻击,借机攻击重击使敌人恍惚,队友晕倒召唤巨蜘蛛
召唤戒指(30英尺内队友伤害检定+2、豁免+2
不渝之志(治疗不引发借机攻击,专注+2,凑数的
生命之纱(体质+6,每天两次治疗重伤,凑数的
蜻蜓链甲(每天一次,30英尺内盟友对恶魔攻击和伤害检定+1,10轮
不宣之实长袍(感知+2环境,10英尺恐惧灵光,dc为25+魅力调整值
摄人巨力(+6力量,15英尺内敌人意志豁免-2
使节手套(沟通+5表现,魅力+2增强
神速靴(运动+10表现,灵巧+5表现
道具栏还是各种权杖,没怎么用过
爱露
永寒(每轮第一次攻击射两箭,若都命中,敌人过dc25强韧,失败1轮恍惚+2d6寒冷伤害
风宗头盔(先攻+4
凶猛契约护目镜(伤害检定+4,感知+2
剥皮斗篷(第一次被击中时过dc29强韧,失败恍惚+1d4轮每轮两点体质流失
锐击戒指(命中近战敌人使其攻击检定-1
无情射杀(近程射击攻击检定+1
突袭护腕(偷袭+1d6钝击伤害
快速应敌护符(对大型及以上敌人攻击和伤害+2洞察,先攻+4
笛拉梅尔的盔甲(树肤cl+2
招摇撞骗(借机攻击检定+2,巧手+10表现
嗜血腰带(杀死敌人后下一次攻击检定+5士气,敏捷和力量+4
精准手套(近程射击+1d6穿刺伤害、流血1d3轮
隆奈克的牺牲(+8敏捷,加速术提供的ac、攻击检定、反射检定加倍
小魔鬼(巧手和隐匿+2亵渎
炽焰弹药箭筒(每天20发,+1d6火焰
玫瑰刺弹药箭筒(每天20发,+2d8污邪,有几率造成无能诅咒
延时权杖
低等延时权杖
第四章收尾+19级+神话7
到女王那坐飞船,路上剧情全部检定成功(否则进入矿井的地点不同,还有可能被扒装备,太麻烦了)
然后出门右拐,一路见到谄媚女王,接任务。然后就是到处清怪了……
有霸烙魔,需要共用防护火焰
有晶簇的地方主角上好寒冰之躯一个人过去解决就好
打黑龙的地方,提前铺炉台守卫,站位分散(它会喷吐aoe),爱露索希尔专心辅助,席拉如果辟邪斩充裕也可以用正义烙印(我没用),主角和兰恩打,兰恩战斗内攻击加值76(如果加上爱露的共享狩猎目标和席拉的正义烙印还可以更高),对方ac88,用上极意击和索希尔的善良之触还是很有可能打中的。主角就用射线法术打就好,龙类传统弱接触攻击。我突袭轮兰恩打了个重击,再下一轮就打死了

 这一层其他的就不难打了,打完回到谄媚女王处交任务,开启小路到下一片地图。这时我升19级了
这一层其他的就不难打了,打完回到谄媚女王处交任务,开启小路到下一片地图。这时我升19级了
19级
主角 博学士 解法余波 高等天使之貌 津波
席拉 突变斗士 踉跄盾击
兰恩 突变斗士 穿透打击 高等穿透打击
聂纽 博学士 高等法术专攻-惑控 德鲁伊法术-凛冬之握 虹光喷射 迷幻图纹
索希尔 牧师 法术专精-秩序护盾
爱露 穷追猛打 精通精准射击
山茶 博学士 额外巫术-祈福 游荡者秘闻-机会主义者
沃尔吉夫 盔甲专攻-轻甲 细剑
鸟哥 突变斗士 穷追猛打 进阶武器训练-枕戈待旦
岱兰 飞翼 自然低语 可怖外表 群体医疗术
葛雷博 杀手 高等双武器战斗 倦惰打击
然后走谄媚女王指出的小道,下一张地图里没什么难打的,主角多放放闪电链就过了,如果没过就再多瞬发一两个。穆塔萨芬可以威吓吓跑。清完的地图应该是下面这样。休息叠餐食加值(给索希尔记一个神圣灵光),准备boss战

boss战
满buff之后主角两个链状闪电就把小怪清了,中间巴弗灭女儿也就兰恩砍几刀的事,索希尔记得上炉台守卫,接下来巴弗灭出场要扒大家buff了,不愧是buff灭呀!不是天使道途也没必要好好打他,撑住三四轮就行了,想飞升记得用午夜之弩射他然后捡水晶。如果是天使道途主角就提前多记点天使道途特有的buff类法术吧,依稀记得以前玩天使僧兵时靠天使buff翻过盘……
打完巴弗灭如果有队友被恶意变形术,先用主角的法术覆盖然后再高等解除魔法
打完拒绝亵渎之礼(我这里是为了后面更容易转传奇道徒)获得险影,还能捡到希望使者不朽的爱,给席拉换上,奔雷腰带我给爱乌了
先不急着走,找谄媚女王交任务+传送下去杀boss战附近的火蜥蜴灼烧灵魂拿到属性+2书,然后再走
神话7
主角:持久法术(获得了五环法术重焕光彩!好耶!
席拉:引领打击
兰恩:引领打击
聂纽:持久法术
索希尔:持久法术
爱露:屹立不倒
山茶:引领打击
沃尔吉夫:持久法术
鸟哥:常备不怠
岱兰:充裕施法
葛雷博:引领打击
回纽系营,只有简单的小战斗,过完剧情就回眷泽城喽!
第五章
眷泽城+神话8+城内休整
回到眷泽城,遇到安妮维亚之前的战斗都不难,遇到安妮维亚之后就可以休息了,后面的休息点也很多,不用太节省,我是打到半份酒馆之后休息了一下
出门记得敲响仁慈之钟,打完两波小怪之后遇到斯陶顿,打完获得戒指 能量之源:每天额引导能量外两次,旁边还能捡到烈火法袍:火属性法术豁免难度+2
再往后会有一个二选一剧情杀,独眼魔鬼和希洛只能选一个救。我目前试出来的保住双方的方法是:先去监狱把监狱门口的战斗打完,然后再去酒馆找独眼魔鬼,最后再来监狱找希洛
小怪都没什么威胁,全部打完之后进要塞,和说书人对话前先到指挥官房间捡到魔法生物的皮,然后对话过剧情
我继续走了灵使道途,主要是为了强度
神话8
主角:偏好超魔(甄选),惊世神力,法术是随便选的
席拉:神话盔甲专攻(回避)
兰恩:精通先攻(神话)
柯米丽雅:持久法术
沃尔吉夫:精通重击(匕首)
聂纽:偏好超魔(甄选)
乌布里格:猛力攻击(神话)
岱兰:精通充裕施法
索希尔:高等持久法术
爱露莎蕾:致命瞄准(神话)
葛雷博:精通重击(神话)(弯刀)
卖垃圾,现在钱完全不会不够用了。军需官处购入大型次元袋。我还在牧师那里买了一些法力珍珠备用。
圣教军:诱人冲动→噬心浪欲;污秽尖啸→无面之声
整理法术位,休息,推进一下道途任务,然后出门战斗喽
大地图支线(1)+兰恩任务+升20级
寒溪村
第一次出门会先遇到苏尔,护送回眷泽城之后重新出来到寒溪村。
首先需要打几只水元素,然后坐船去小岛,路上需要过检定。到小岛拆掉很多陷阱之后可以选择打鬼婆,也可以选择说服她们。
怪脊村(dlc)
我第五章才来这里,所以很好打,没什么说的,废墟里的解谜是两边各放一个钻石
兰恩个人任务
同样不难打,打完获得武器萨瓦米勒克之脊(复合长弓),兰恩获得力量+2、体质+2、毒素豁免+4
白骨丘
有一群食魂魔,上完防死结界丢法术乱杀,打完获得最终面纱解谜道具
最终面纱
解谜,获得一张精灵笔记
欢笑洞窟
外侧地图不难打,打完有一把决斗剑冻血者。洞窟内部有霸烙魔,需要防火buff,打完获得神秘之心解谜道具
我打到这里就20级了,正好也该回眷泽城了,回去路上触发了小烬任务
升20级
主角:神威如岳
席拉:原怒者-魅力-天界
兰恩:力量-动如脱兔-长柄
索希尔:牧师,专精秩序护盾
聂纽:博学士-敏捷-复仇旋风,另一个随便学的
爱露纱蕾:魅力


























 感觉大家在海边的状态都好放松,很悠闲。我就站在那里看着来来往往的人群,听着海浪翻滚的声音,也觉得内心变得无比平静。
感觉大家在海边的状态都好放松,很悠闲。我就站在那里看着来来往往的人群,听着海浪翻滚的声音,也觉得内心变得无比平静。


 最后看完了日落,我们就动身回宾馆收拾东西啦~
最后看完了日落,我们就动身回宾馆收拾东西啦~






















 右侧有会放臭云术的赘行魔,嫌被控难受的话,可以在快进它视线范围内的时候停下来,等伊拉贝思那边的人打完左侧过来替我们吃。或者席拉先去骗它出招。这段战斗的重点不是输出而是少掉血。
右侧有会放臭云术的赘行魔,嫌被控难受的话,可以在快进它视线范围内的时候停下来,等伊拉贝思那边的人打完左侧过来替我们吃。或者席拉先去骗它出招。这段战斗的重点不是输出而是少掉血。


 追问是谁获得额外经验,然后过运动检定救人,sl通过检定,让他们去找伊拉贝思。
追问是谁获得额外经验,然后过运动检定救人,sl通过检定,让他们去找伊拉贝思。 目前经验12682/15000,buff剩余时间不到一分半(如果经验不够,注意看地图中的技能检定是不是都过了)
目前经验12682/15000,buff剩余时间不到一分半(如果经验不够,注意看地图中的技能检定是不是都过了) 旁边的房子之后再来,因为需要用到防死结界卷轴,目前还没买。
旁边的房子之后再来,因为需要用到防死结界卷轴,目前还没买。



 目前经验19220
目前经验19220



 过去之后往前走,看到敌人再开始上buff,对速袭魔依旧可以用致盲射线,对会隐形的法师依旧用闪光尘,有两个速袭魔的地方 凛冬之握/油腻术/刺耳尖啸之类的控制法术也可以交一下
过去之后往前走,看到敌人再开始上buff,对速袭魔依旧可以用致盲射线,对会隐形的法师依旧用闪光尘,有两个速袭魔的地方 凛冬之握/油腻术/刺耳尖啸之类的控制法术也可以交一下






 然后随便逛逛清清怪就走了。
然后随便逛逛清清怪就走了。
 至于打法,我用了闪光尘+臭云术,兰恩砍中了再恐惧几个,就好处理了。打完察觉到房间右上的暗门(如图)
至于打法,我用了闪光尘+臭云术,兰恩砍中了再恐惧几个,就好处理了。打完察觉到房间右上的暗门(如图) 

 在这里主角又扔了臭云术,岱兰用了操纵亡者(不用太节省,打boss之前会贴心地回复所有法术位的)。我打完这里的时候每等级一分钟的buff差不多要掉了,捡捡东西休息一下,这次记得休息前记加速术(捡到一个+2敏捷腰带可以给兰恩,+2巨力腰带和骤然巨力可以给席拉)。
在这里主角又扔了臭云术,岱兰用了操纵亡者(不用太节省,打boss之前会贴心地回复所有法术位的)。我打完这里的时候每等级一分钟的buff差不多要掉了,捡捡东西休息一下,这次记得休息前记加速术(捡到一个+2敏捷腰带可以给兰恩,+2巨力腰带和骤然巨力可以给席拉)。
 满buff,给席拉法师护甲,用上黑暗罩纱,开门。
如果有dlc2:第一轮用夺命暴雪权杖对boss上魔法飞弹,造成缓慢术效果,让她放不出虫群。席拉兰恩集火boss尽快杀掉。
如果没有dlc2:用防护箭矢抵消集群伤害,同样集火boss。
满buff,给席拉法师护甲,用上黑暗罩纱,开门。
如果有dlc2:第一轮用夺命暴雪权杖对boss上魔法飞弹,造成缓慢术效果,让她放不出虫群。席拉兰恩集火boss尽快杀掉。
如果没有dlc2:用防护箭矢抵消集群伤害,同样集火boss。

 一开始不要走得离冥娜蛊太近不然她会传送走,在龙傲天buff下我们的法术dc会非常高,所以可以先用法术控住她(主要目的是让她不要放出来腐烂幻象)。打到一定程度之后出现第二波小怪,这波小怪的初始仇恨在主角身上,很烦,也可以提前铺一些地形法术控住,优先集火冥娜蛊,把冥娜蛊血条打空触发剧情之后怪就都走了
一开始不要走得离冥娜蛊太近不然她会传送走,在龙傲天buff下我们的法术dc会非常高,所以可以先用法术控住她(主要目的是让她不要放出来腐烂幻象)。打到一定程度之后出现第二波小怪,这波小怪的初始仇恨在主角身上,很烦,也可以提前铺一些地形法术控住,优先集火冥娜蛊,把冥娜蛊血条打空触发剧情之后怪就都走了




 黑暗之角先给索希尔拿着了,黑镜护符给了小烬
黑暗之角先给索希尔拿着了,黑镜护符给了小烬


 圣教军现在是这样。去寒溪村,搜刮一圈,地图右边的动物可以打一打,和月舞草原差不多
圣教军现在是这样。去寒溪村,搜刮一圈,地图右边的动物可以打一打,和月舞草原差不多
 打完(老雷打完)捡到灵感头带,可以先给兰恩戴,之后带山茶的时候换给山茶
打完(老雷打完)捡到灵感头带,可以先给兰恩戴,之后带山茶的时候换给山茶



 不小心让岱兰被中了debuff的兰恩砍死了一次,用掉了银龙鳞片,不过之前给说书人看过鳞片了,应该不会卡任务。
前半段的buff就是常规buff,唯一要注意的只是让索希尔给兰恩上圣战之刃,获得额外附伤,打集群打得快一点;聂纽之前记的冰风暴可以换回高等隐形术了。
有四个集群埋伏的地方,可以让动物伙伴去一侧送,暂时拖住两个集群,防止大部队被集群集火aoe暴毙。
接下来休息一下就去打尸妖那条路。目前经验50198/51000,快升8级了
不小心让岱兰被中了debuff的兰恩砍死了一次,用掉了银龙鳞片,不过之前给说书人看过鳞片了,应该不会卡任务。
前半段的buff就是常规buff,唯一要注意的只是让索希尔给兰恩上圣战之刃,获得额外附伤,打集群打得快一点;聂纽之前记的冰风暴可以换回高等隐形术了。
有四个集群埋伏的地方,可以让动物伙伴去一侧送,暂时拖住两个集群,防止大部队被集群集火aoe暴毙。
接下来休息一下就去打尸妖那条路。目前经验50198/51000,快升8级了 8级:
主角:魅力,咆哮术
席拉:圣武士,魅力,眩晕(随便选的)
兰恩:力量,精通重击(斩矛),菲尼安可以变斩矛给兰恩用了,碎虫者可以卖了
聂纽:智力,虹彩图纹,灭顶悲痛(感觉选得不太好,都是打意志的法术,不过主角已经学了咆哮术打强韧了,而且四环打反射的法术也不多,聂纽也学了火球术了……)
索希尔:感知
岱兰:魅力,行动自如
山茶:敏捷,冻皮
沃尔吉夫:敏捷,战斗特技-精通双武器战斗,加速术,英雄气概
烬:魅力,救难,防死结界
鸟哥:力量
狼:力量
8级:
主角:魅力,咆哮术
席拉:圣武士,魅力,眩晕(随便选的)
兰恩:力量,精通重击(斩矛),菲尼安可以变斩矛给兰恩用了,碎虫者可以卖了
聂纽:智力,虹彩图纹,灭顶悲痛(感觉选得不太好,都是打意志的法术,不过主角已经学了咆哮术打强韧了,而且四环打反射的法术也不多,聂纽也学了火球术了……)
索希尔:感知
岱兰:魅力,行动自如
山茶:敏捷,冻皮
沃尔吉夫:敏捷,战斗特技-精通双武器战斗,加速术,英雄气概
烬:魅力,救难,防死结界
鸟哥:力量
狼:力量 主角第二轮可以补一个渐隐术,因为第二轮石像鬼的初始仇恨在主角身上,可以提前让兰恩站在石像鬼到主角身边的路上,借机攻击蹭点伤害
主角第二轮可以补一个渐隐术,因为第二轮石像鬼的初始仇恨在主角身上,可以提前让兰恩站在石像鬼到主角身边的路上,借机攻击蹭点伤害


 捡到嗅血斗篷给兰恩装备,神圣轻弩可以先留着(后面看要不要给爱露用),其他新捡到的装备我都卖了。目前金币33600+,经验88599/105000。
捡到嗅血斗篷给兰恩装备,神圣轻弩可以先留着(后面看要不要给爱露用),其他新捡到的装备我都卖了。目前金币33600+,经验88599/105000。
 监狱里面还有一个会隐身的,还是闪光尘。半魔界牛头人ab比较高,可以交一个辟邪斩,提前走得离他近一点他就不容易冲锋。
打完把赘行魔放出来,拿到他身上的钥匙。目前教堂酒馆监狱三把钥匙已经集齐了。
和爱露对话,唱歌,爱露入队(但先不带她
开隐藏墙后面的敌人有点麻烦,我又用了一张腐烂幻象
监狱里面还有一个会隐身的,还是闪光尘。半魔界牛头人ab比较高,可以交一个辟邪斩,提前走得离他近一点他就不容易冲锋。
打完把赘行魔放出来,拿到他身上的钥匙。目前教堂酒馆监狱三把钥匙已经集齐了。
和爱露对话,唱歌,爱露入队(但先不带她
开隐藏墙后面的敌人有点麻烦,我又用了一张腐烂幻象










 再往前房间的毒啮魔弱强韧,主角用甄选咆哮术,六臂蛇魔ab比较高,真顶不住就等休息完再来用屹立不倒顶
另一个房间的纳祭魔,打法1开局迅速控+杀其他小怪防止它们控制队友/扰乱战局,再和纳祭魔硬碰硬,它造成的眩晕用席拉的圣疗解决。打法2开局迅速集火在纳祭魔上完buff之前秒了它(需要运气,我兰恩不到两轮出了三次重击才秒掉)。都用上了炉台守卫。旁边房间的袍泽头盔给席拉戴上
再往前房间的毒啮魔弱强韧,主角用甄选咆哮术,六臂蛇魔ab比较高,真顶不住就等休息完再来用屹立不倒顶
另一个房间的纳祭魔,打法1开局迅速控+杀其他小怪防止它们控制队友/扰乱战局,再和纳祭魔硬碰硬,它造成的眩晕用席拉的圣疗解决。打法2开局迅速集火在纳祭魔上完buff之前秒了它(需要运气,我兰恩不到两轮出了三次重击才秒掉)。都用上了炉台守卫。旁边房间的袍泽头盔给席拉戴上

 左上角洞穴里的索亚纳可以喂山茶(但我没喂
离开地图,回眷泽城。卖垃圾,对话完成任务,找塞珥。
军需官给指挥官礼物了
找兰恩和苏尔对话,触发兰恩做酋长事件
现在已经存下13万了,下次做猎龙任务和鸟哥任务,正好雇一下葛雷博,再在鸟哥地图商人那里花花钱
左上角洞穴里的索亚纳可以喂山茶(但我没喂
离开地图,回眷泽城。卖垃圾,对话完成任务,找塞珥。
军需官给指挥官礼物了
找兰恩和苏尔对话,触发兰恩做酋长事件
现在已经存下13万了,下次做猎龙任务和鸟哥任务,正好雇一下葛雷博,再在鸟哥地图商人那里花花钱
















 雷吉尔任务地图满buff就很好打,捡到速杀匕首给小狗贼用。
雷吉尔任务地图满buff就很好打,捡到速杀匕首给小狗贼用。





 拿到恶魔愤恨给兰恩戴。打完就可以走了,这次回去路上必定触发卓尔精灵的任务事件,记得提前留好buff/休息一下
当前经验418458/445000,又快能升14级了
拿到恶魔愤恨给兰恩戴。打完就可以走了,这次回去路上必定触发卓尔精灵的任务事件,记得提前留好buff/休息一下
当前经验418458/445000,又快能升14级了 再往前,看到增强火蜥蜴,杀,捡东西,拿到炸弹(但不想捡东西的话应该也可以不杀……?反正这边有用的只有用来开门的炸弹,而门可以用密码开),回到正门口,这次向左走,两侧的门先不用开,一路往前走
再往前,看到增强火蜥蜴,杀,捡东西,拿到炸弹(但不想捡东西的话应该也可以不杀……?反正这边有用的只有用来开门的炸弹,而门可以用密码开),回到正门口,这次向左走,两侧的门先不用开,一路往前走
 目前地图右下角彻底探索后是这个样子:
目前地图右下角彻底探索后是这个样子:
 刚才有火蜥蜴的房间门外的敌人忘记对话了,对话获得密码前两位:
刚才有火蜥蜴的房间门外的敌人忘记对话了,对话获得密码前两位:
 现在大门可以打开了。打开之后来到图示位置,前面圆环型平台上的战斗是第一处有难度的战斗。
现在大门可以打开了。打开之后来到图示位置,前面圆环型平台上的战斗是第一处有难度的战斗。




 目前聂纽的法穿有了灵使的+4法穿buff之后就也够打小精英怪了,惑控和幻术系法术的dc也够用。反正有德莱文的帽子,一发没控住还可以瞬发补一下。主角的咆哮术超魔后dc更高,还有卓越魔法,很好控。
圆环平台上的敌人还有电击抗性,我这里打倒之后用召雷魔杖/电戏法补刀有可能过不去电抗。但精金也可以破再生,所以说可以准备精金武器。看别人说等敌人倒地之后用致命一击也可以,我没试过。
(发现共用防护箭矢卷轴用完了,记得之后做一点备用)
目前聂纽的法穿有了灵使的+4法穿buff之后就也够打小精英怪了,惑控和幻术系法术的dc也够用。反正有德莱文的帽子,一发没控住还可以瞬发补一下。主角的咆哮术超魔后dc更高,还有卓越魔法,很好控。
圆环平台上的敌人还有电击抗性,我这里打倒之后用召雷魔杖/电戏法补刀有可能过不去电抗。但精金也可以破再生,所以说可以准备精金武器。看别人说等敌人倒地之后用致命一击也可以,我没试过。
(发现共用防护箭矢卷轴用完了,记得之后做一点备用) 小boss这边敌人ac没有刚才那么高,需要和装置互动解除屏障才能打到高台上的敌人。弓箭手比较烦,黑暗罩纱也可以用一下,以防后排被射中
小boss这边敌人ac没有刚才那么高,需要和装置互动解除屏障才能打到高台上的敌人。弓箭手比较烦,黑暗罩纱也可以用一下,以防后排被射中 我玩到这里的时候加速术移位术高等隐形术buff用完了,休息一下
我玩到这里的时候加速术移位术高等隐形术buff用完了,休息一下



































 ……结果就这样把岛10打完了,不够的辅助用药水和索希尔的领域能力来凑,最后交了炉台守卫(第三章以来大家的法术位用得最干净的一次),地图末尾刚好有雕像恢复状态。战利品如图,岛9的眼镜和这里的长袍适合智力系法师,给聂纽了
……结果就这样把岛10打完了,不够的辅助用药水和索希尔的领域能力来凑,最后交了炉台守卫(第三章以来大家的法术位用得最干净的一次),地图末尾刚好有雕像恢复状态。战利品如图,岛9的眼镜和这里的长袍适合智力系法师,给聂纽了



 战利品如图,还有一个猛击之盾,但感觉不如席拉现在用着的凯旋正午
战利品如图,还有一个猛击之盾,但感觉不如席拉现在用着的凯旋正午

























 打完获得弯刀火风暴,给席拉
打完获得弯刀火风暴,给席拉
 之前在灵使花园上的分钟级buff也刚好掉光了,那就休息一下再打其他小怪吧,下次再玩
之前在灵使花园上的分钟级buff也刚好掉光了,那就休息一下再打其他小怪吧,下次再玩


 现在有dlc4的集群克星搭扣就舒服很多,还有主角的巅峰元素火……还记得我第一次玩核心难度的时候还没有带小烬,没人扔火球术,好像是靠前面恶魔掉的津波卷轴sl无数次杀掉的……总之主角和兰恩依旧是输出的大头,打打就过了……主要战利品如图
现在有dlc4的集群克星搭扣就舒服很多,还有主角的巅峰元素火……还记得我第一次玩核心难度的时候还没有带小烬,没人扔火球术,好像是靠前面恶魔掉的津波卷轴sl无数次杀掉的……总之主角和兰恩依旧是输出的大头,打打就过了……主要战利品如图

 没有dlc4的可以先打取乐的黑暗,打完获得一个集群克星搭扣给兰恩
没有dlc4的可以先打取乐的黑暗,打完获得一个集群克星搭扣给兰恩
 总之开战之前能上的buff都上了,炉台守卫我前面用掉了不然我这里一定会上,索希尔在取乐的黑暗那边召唤骷髅开战,这样它前两三局会先挠骷髅(和阴影宽恕给的巨蜘蛛,只要骷髅死亡就会出现)
总之开战之前能上的buff都上了,炉台守卫我前面用掉了不然我这里一定会上,索希尔在取乐的黑暗那边召唤骷髅开战,这样它前两三局会先挠骷髅(和阴影宽恕给的巨蜘蛛,只要骷髅死亡就会出现)

 索希尔和主角使用解除魔法,解到最后是下图p1这个情况(此时它才刚刚把召唤物全杀光,走到席拉面前),此时兰恩搭配索希尔的领域辅助就可以命中了,席拉用屹立不倒顶住就好(主角还可以扔正义烙印加持下的魔法飞弹),这之后两回合就杀掉了,获得经验52224,又快要升16级了
索希尔和主角使用解除魔法,解到最后是下图p1这个情况(此时它才刚刚把召唤物全杀光,走到席拉面前),此时兰恩搭配索希尔的领域辅助就可以命中了,席拉用屹立不倒顶住就好(主角还可以扔正义烙印加持下的魔法飞弹),这之后两回合就杀掉了,获得经验52224,又快要升16级了












































 打完看完剧情再逛一下房间,我让沃尔吉夫拒绝力量,捡到了招摇撞骗
打完看完剧情再逛一下房间,我让沃尔吉夫拒绝力量,捡到了招摇撞骗 我打完打累了不想打了,去把约会任务做完获得传送金币、维勒西亚的调节护符(给主角)和大量经验。
我打完打累了不想打了,去把约会任务做完获得传送金币、维勒西亚的调节护符(给主角)和大量经验。


 其实还没休息,现在顺便在法师塔休息一下好了……!休息完出法师塔,把旁边的吸血鬼xxx打一下(上防死结界和黑暗罩纱
其实还没休息,现在顺便在法师塔休息一下好了……!休息完出法师塔,把旁边的吸血鬼xxx打一下(上防死结界和黑暗罩纱


 可以根据需要选择,其中斗篷的效果会根据道途有所不同。我选的是靴子,给了小狗),只带会寒冰之躯的队友(我这边就是主角和聂纽),用上寒冰之躯免疫食肉晶簇的控制效果然后法术轰炸,比带上所有队友更好打。
可以根据需要选择,其中斗篷的效果会根据道途有所不同。我选的是靴子,给了小狗),只带会寒冰之躯的队友(我这边就是主角和聂纽),用上寒冰之躯免疫食肉晶簇的控制效果然后法术轰炸,比带上所有队友更好打。

















 之后如果不考虑rp的话就坐女王的飞船去最保险。接下来我要做坏东西,把不需要的npc都杀掉了。
传送到厄运酒馆,杀米勒拉,获得两件惑控法装备,都可以给聂纽
奴隶市场的另一个船长不知道去哪了,那就不杀了。
休息一下,去dlc3了!
之后如果不考虑rp的话就坐女王的飞船去最保险。接下来我要做坏东西,把不需要的npc都杀掉了。
传送到厄运酒馆,杀米勒拉,获得两件惑控法装备,都可以给聂纽
奴隶市场的另一个船长不知道去哪了,那就不杀了。
休息一下,去dlc3了!













 回去找说书人补充一下卷轴,再休息一下就去女王那坐飞船了,队伍是主角席拉兰恩聂纽爱露索希尔。这次不用叠餐食加值,因为反正会掉(
回去找说书人补充一下卷轴,再休息一下就去女王那坐飞船了,队伍是主角席拉兰恩聂纽爱露索希尔。这次不用叠餐食加值,因为反正会掉(
 这一层其他的就不难打了,打完回到谄媚女王处交任务,开启小路到下一片地图。这时我升19级了
这一层其他的就不难打了,打完回到谄媚女王处交任务,开启小路到下一片地图。这时我升19级了